Saïp Ciss∗
September 22, 2014
September 22, 2014
- 1 Introduction
- 2 Random uniform decision trees
- 3 Random Uniform Forests
- 4 Some extensions
- 5 Examples
- 6 Conclusion
5 Examples
Random Uniform Forests를 사용하여 작업이 어떻게 수행되는지 완전한 짧은 예제를 이 절에서 보여준다.
Usage in R
randomUniformForest 패키지의 참조 매뉴얼은 알고리즘에서 옵션을 사용하고 다룰 수 있는 모든 상세한 방법을 제공한다. 아래의 라인에서, 사용된 옵션을 언급한다.
패키지를 설치하기 위해:
install.packages("randomUniformForest")
패키지를 적재하기 위해:
library(randomUniformForest)
Methods
randomUniformForest 패키지, 버전 1.0.08을 비교하기 위해 사용했다,
- 패키지 randomUniformForest(Liaw, Wiener, 2002), 원본의 Breiman 절차를 따라 구현됨,
- 패키지 extraTrees (Simm, de Abril, 2013), 극대화 임의 트리(Extremely Randomized Trees) 알고리즘을 자유롭게 구현,
- 패키지 e1071 (Meyer et al.), SVM (Support Vector Machines) (Vapnik, Cortes, 1995)을 구현,
- 패키지 gbm (Ridgeway et al.), radient Boosting Machines (Friedman, 2001, 2002)을 구현.
다른 정확한 모델은 R에서서 사용가능함에 주목, BayesTree, ipred, glmnet, rpart, kernlab, klar,.. 등. Rdocumentation 또는 CRAN Task View: Machine Learning and Statistical Learning 에서 더 있음.
10-배 교차 검증을 대부분 비교에서 사용했다, 각 데이터 집합에서, 같은 seed (2014로 설정)를 사용했다, R 코드 set.seed(2014)를 각 프로지저 전에 호출, 모두에게 같은 결과를 보이기 위해, 그리고 모든 데이터는 UCI 저정소: http://archive.ics.uci.edu/ml/index.html에서 이용 가능하다
단순한 방법으로 어떻게 작동되는지 보여주기 위해, 가능한 자주 R 코드를 제공하다.
gbm, extraTrees 그리고 randomUniformForest 같은 어떤 알고리즘에서 같은 시드의 사용해도 같은 데이터에서 다른 결과가 나타남은 무작위가 원인이다. 수렴을 얻기 위해 알고리즘은 충분한 트리(≥ 200)를 가져야 한다.
5.1 Classification
Random Uniform Forests의 다른 수단을 설명하기 위해 매 번 하나의 주제에 사용하기 위해 UCI 저장소에서 이용 가능한 4개의 데이터셋을 평가한다.
5.1.1 Iris data (assessment of variable importance)
Iris 데이터는 기계 학습에서 가장 유명한 것들 중 하나이다. 상세한 보고: 이 유명한 (Fisher’s or Anderson’s) iris 데이터 셋은 다양한 꽃받침 길이와 넓이, 꽃잎의 길이와 넓이를 센티미터로 측정되어 제공한다, iris의 각각 3개 종에서 50 개의 꽃을 개별적으로. 종은 아이리스 세토사(setosa), 버시칼라(versicolor), 버지니카(virginica)이다.
# load the algorithm and data
library(randomUniformForest)
data(iris)
XY = iris
# column of the classes
classColumn = 5
# separate data from labels
Y = extractYFromData(XY, whichColForY = classColumn)$Y
X = extractYFromData(XY, whichColForY = classColumn)$X
# run model: default options
ruf = randomUniformForest(X, Y = as.factor(Y))
# display results...
ruf
# ...gives standard output (below) of a Random Uniform Forest
Call:
randomUniformForest.default(X = X, Y = as.factor(Y))
Type of random uniform forest: Classification
paramsObject
ntree 100
mtry 5
nodesize 1
maxnodes Inf
replace TRUE
bagging FALSE
depth Inf
depthcontrol FALSE
OOB TRUE
importance TRUE
subsamplerate 1
classwt FALSE
classcutoff FALSE
oversampling FALSE
outputperturbationsampling FALSE
targetclass -1
rebalancedsampling FALSE
randomcombination FALSE
randomfeature FALSE
categorical variables FALSE
featureselectionrule entropy
Out-of-bag (OOB) evaluation
OOB estimate of error rate: 4%
OOB error rate bound (with 1% deviation): 4.88%
OOB confusion matrix:
Reference
Prediction setosa versicolor virginica class.error
setosa 50 0 0 0.00
versicolor 0 47 3 0.06
virginica 0 3 47 0.06
OOB geometric mean: 0.9596
OOB geometric mean of the precision: 0.9596
Breiman’s bounds
Prediction error (expected to be lower than): 0.37%
Upper bound of prediction error: 3.84%
Average correlation between trees: 0.0176
Strength (margin): 0.9096
Standard deviation of strength: 0.1782
- RandomForest 패키지에서와 같이 정의된 어떤 옵션을 주목할 수 있다, 같은 인수(argument)를 의미(트리 개수를 위한 ntree, 각 노드에서 묶여질 변수의 수를 위한 mtry, 각 노드에서 관측의 최소 수를 위한 nodesize).
- 다음 라인은 OOB 오류, 혼동 메트릭(confusion matrix) 그리고 추정을 평가하는 어떤 측정을 가지고 OOB 평가를 제공한다.
- 마지막 그룹은 Breiman’s bounds와 그들의 상세이다. OOB 오류는 어떤 Breiman’s bound 안에 있지 않음을 여기서 주목할 수 있다. 과적합이 쉽게 발생할 수 있음을 나타낸다 그리고 예측 오류의 결론 전에 더 많은 데이터를 가져야 한다, 그래서 짝 관측에서(pairwise observations) margin과 상관관계를 추정하기 위해 필요하다, 평가에 사용된 것 보다 작은 경우에 나타남.
그러면, 공변량이 종을 어떻게 설명하는지에 집중한다. 처음 단계로 모델이 (기본으로) 가지는 전역 변수 중요도(global variable importance)를 제공한다.
# call the summary() function gives some details about the forest and # global variable importance summary(ruf)
 |
| Figure 1: iris 데이터 셋에서 전역 변수 중요도 |
그림은 모든 변수의 상관 영향을 보여준다. 수직 선(회색)은 모든 변수가 같은 영향을 가진다면 영향이 있는 위치를 보여준다. 그러나, 중요한 변수가 무엇인지를 앎이 하나의 종과 다른 종을 설명하는 것이 무엇인지 우리에게 알려주지 않는다. 그래서, 상세에 접근한다.
# assess the details of variable importance # we set ’maxInteractions’ to its highest level, # i.e., the dimension of the problem imp.ruf = importance(ruf, Xtest = X, maxInteractions = 4) # then, see the big picture (please use vertical tiling in the R menu # to see all plots) plot(imp.ruf, Xtest = X)
 |
| Figure 2: iris 데이터셋에서, 상호 작용에 기반한 변수 중요도 그리고 상호 작용 |
상호작용 시각화는 모델과 데이터 모두에서 더 의존하며 변수 중요도를 평가하는 첫번째 수단이다. 여기서 첫번째 또는 두번째 위치에 있는 종료 노드에 존재하는 변수를 셈한다. 모델에 더 많은 작업을 요청한다 그래서 각 트리의 대부분은 셈하기 전에 필요하지만, 그러나 오로지 트리의 반(종료 노드)만 사용된다. 임의성은 제약이 되고, 상호작용이 다른 하나를 생성함에 따라, 같은 변수는 충분히 중요하게 되는 두번째 순서(위치)에 다시 발생이 요구됨으로써. 발생 빈도의 셈은 데이터에 더 의존한다 그래서 모든 잠재적인 예측자(모든 트리에서)는 포함된다. 이 책략은 관측에서 변수 중요도(Variables interactions over observations)를 제공한다. 하나는 Petal.width 와 Petal.Length가 대부분의 상호작용을 이끄는 것으로 볼 수 있다 그렇지만 Sepal.Length는 어떤 다른 변수와 상호작용을 가지지 않는다.
모자이크 플롯(mosaic plot)은 그들의 중요도로 변수를 정렬한다. 첫번째 정렬은 열에서 첫번째 변수는 가장 중요하다, 두번째 변수가 따라옴 그리고 등등. 두번째 정열은 첫번째 열에서 첫번째 변수 보다 더 중요한 다른 (알려지지 않은) 변수이다. 만약, 예로, 그것이 대부분 경우에 중요하다면 이 알려지지 않은 변수는, 어쨌든, 두번째 정렬에 나타날 수 있다. 단순히, 상호작용을 계산하여 취할 때, 첫번째와 두번째 정렬에서 가장 앞의 변수는 보통 가장 중요하다, 그러나 그것은 항상 중요하지는 않다 그리고 규칙이 없다. 여기서 우리는 많은 변수를 가지지 않는다. Petal.Length는 강한 영항을 가진다 그리고 결과적으로, 두번째 정렬 뷰에서 가장 위의 변수를 확인하면, 그것을 얻을 수 있다 그러나 가장 중요한 변수는 아니다. Petal.Length가 아마도 분류의 대부분에서 영향을 가진다고 우리에게 보여준다, 그렇지만 전체에서 가강 강하지는 않다.
상호작용 집계는 상호 작용에 기반한 변수 중요도(Variable importance based on interactions)를 제공한다. 전역 변수 중요도 측정 보다 분류 간에 가장 잘 분할하도록 이끌 수 있는 잠재적인 변수를 계산하여 취하는 변수 중요도이다.
다른 뷰에서 그들을 보여주기 위해, 하나는 다른 그림으로 제공되는 구별에서의 변수 중요도(Variable importance over labels)를 볼 수 있다.
 |
| Figure 3: iris 데이터셋에서 구별(label)에서 변수 중요도 |
각 구별(Class)에서, 더 깊게 분석하여 어떤 변수가 중요한지 확인한다. Petal.Length는 2개의 종에서 중요하다고 설명한다 그렇지만 Petal.Width가 마지막 구별을 더 잘 설명한다. Sepal.Width는 그것의 상호작용에서만 중요하게 남아있다 그러고, 여기서, 그것의 기여하지는 않는다.
그러나 Sepal.Length는 무엇을 말하는가? 왜 그것이 정보를 제공하지 않는지 알기를 원할 것이다. 같은 경우에, 왜 다른 변수는 그렇게 중요한지 알기를 원할 것이다. 이것을 위해, 모든 변수에서 부분 의존도(partial dependencies)를 얻는다 (위의 플롯의 호출은 단지 가장 중요한 변수를 사용자가 선택하기 위해 단지 부분 중요도를 그릴 뿐이다, 입력에서, 그가 그리기를 원하는 변수).
 |
| Figure 4: 꽃잎 길이와 넓이에서 부분 의존도 |
부분 중요도의 주요 요지은 종들(classes) 간에 분할하도록 이끄는 어떤 것을 보기 위해서 이다, 그리고 쉽게 구별을 하든지 안하든지 상관 없음. 예로, 여기서, Petal.Length가 2 아래에 있고 Petal.Width가 0.5 아래에 있으면, 큰 확률을 가지고 종은 Setosa이다. 그러면, 오로지 단지 2개의 변수만으로 종을 구별하기에 충분하다. 무엇이 다른 것인가? 더 잠재적인 의존을 얻기 위해 단지 중요한 객체를 가지고 함수를 호출한다:
# for the ’Sepal.Length’ variable
pD.Sepal.Length = partialDependenceOverResponses(imp.ruf, Xtest = X,
whichFeature = "Sepal.Length",
whichOrder = "all")

|
| Figure 5: 꽃받침 폭과 길이에서 부분 의존도 |
Sepal.Width 와 Sepal.Length는 더 작은 판별 변수이다 그러면 덜 중요하다고 받아 들인다. 둘의 중요한 차이는 위에서 작성한 바와 같이, Sepal.Width는 다른 변수에서 더 중요하게 여긴다.
각 분류에 대해 충분하게 설명하는데 필요한 변수(예로 많은 변수가 있으면)에 대해 결정하기를 원할 것이다. 부분 중요도가 정보를 제공하도록 단순히 명령한다.
# for the setosa and virginica species pImp.setosa = partialImportance(X, imp.ruf, whichClass = "setosa") pImp.virginica = partialImportance(X, imp.ruf, whichClass = "virginica")
 |
| Figure 6: 구분 setosa와 virginica에서 부분 중요도 |
부분 중요도(Partial importance)는 Petal.Length가 구분 setosa를 알기에 충분하다고 나타낸다 하지만 구분 virginica는 가장중요한 Petal.Width와 그리고 덜 중요한 Petal.Length가 필요하다.
단일 결정 트리에서 어떻게 선호되는지 비교하기를 원할 것이다. 이후의 다른 중요한 기능의 하나는 쉽게 이해할 수 있는 규칙을 제공해야 한다. 그러므로 Random Uniform Forests에서 트리는 강한 임의성이다 (결정론적인(deterministic) CART와 달리), 하나의 트리 시각화는 해석에 적합하지 않다 그리고 다른 트리보다 더 좋은 트리는 없다.
# get a tree tree_100 = getTree.randomUniformForest(ruf,100) # plot a tree in the forest plotTree(tree_100, xlim = c(1,18), ylim = c(1,11))
 |
| Figure 7: forest에서 2개의 트리. 구별 {1,2,3}은 {setosa, versicolor, virginica}이다 |
하나는 규칙이 달라지고 그리고 트리는 깊고 크게 될 수 있음을 볼 수 있다. 그러므로 Random Uniform Forests에서 흥미로운 하나는 bayesian framework이다. 데이터는 고정되고, 변수는 무작위이다. 무작위를 사용하여 거의 모든 변수를 생성한다(그러므로 빠르게 수렴이 발생한다) 그리고 데이터는 많은 다른 구조의 공간에 놓여 있게 한다. 변수 중요도의 경우에, 강한 임의성은 우리가 얻는 효과가 아마도 임의적이지 않거나 특별한 형상을 기대할 수 없음을 보장한다.
5.1.2 Vehicle data
우리가 평가하는 다음 데이터셋은 UCI 저장소 또는 mlbench R 패키지를 이용하여 또한 사용 가능하다. 다음에 설명, 저자 제공. 목적은 4개의 자동차 중 하나로 주어진 형상을 가지고 분류해야 한다, 형상에서 추출된 특징 집합. 자동차는 많은 다른 각도에서 조사되었다.
데이터셋은 946개 관측, 18개의 속성 그리고 4개의 구별을 가진다.
여기서, Random Uniform Forests의 예측 오류를 간단히 평가한다, Random Forests, Extra-Trees 그리고 Gradient Boosting Machines과 비교.
여기서, Random Uniform Forests의 예측 오류를 간단히 평가한다, Random Forests, Extra-Trees 그리고 Gradient Boosting Machines과 비교.
1 - 첫번째 단계에서 하나의 훈련과 검증 집합을 사용한다 그다음 모델이 어떻게 동작하는지 알아 본다.
data(Vehicle, package = "mlbench")
XY = Vehicle
# column of the classes
classColumn = 19
# separate data from labels
Y = extractYFromData(XY, whichColForY = classColumn)$Y
X = extractYFromData(XY, whichColForY = classColumn)$X
# reproducible code and train sample (50%)
set.seed(2014)
train_test = init_values(X, Y, sample.size = 1/2)
# training sample
X1 = train_test$xtrain
Y1 = train_test$ytrain
# test sample
X2 = train_test$xtest
Y2 = train_test$ytest
# run model: default options, but setting number of trees to 500
ruf.vehicle = randomUniformForest(X1, as.factor(Y1),
xtest = X2, ytest = as.factor(Y2), ntree = 500)
# call
ruf.vehicle
# displays
# ...
Out-of-bag (OOB) evaluation
OOB estimate of error rate: 24.35%
OOB error rate bound (with 1% deviation): 27.53%
OOB confusion matrix:
Reference
Prediction bus opel saab van class.error
bus 93 3 4 1 0.0792
opel 0 51 30 0 0.3704
saab 1 41 67 4 0.4071
van 1 10 8 109 0.1484
OOB geometric mean: 0.7271
OOB geometric mean of the precision: 0.7356
Breiman’s bounds
Prediction error (expected to be lower than): 21.97%
Upper bound of prediction error: 35%
Average correlation between trees: 0.0782
Strength (margin): 0.5124
Standard deviation of strength: 0.3031
#...
Test set
Error rate: 26%
Confusion matrix:
Reference
Prediction bus opel saab van class.error
bus 119 2 4 0 0.0480
opel 0 41 29 0 0.4143
saab 0 61 68 0 0.4729
van 4 3 7 85 0.1414
Geometric mean: 0.6951
Geometric mean of the precision: 0.7088
우리는 과적합이 발생했음을 관찰한다. 과적합을 Breiman's bound (21.97%)를 사용하여 알 수 있다, 이것은 OOB 오류의 상단 경계에 있어야 함. 그러나 관계는 단지 한 방향으로만 동작한다. OOB는 Breiman 경계 보다 아래에 있을 수 있다 그리고 과적합을 방지하지 않는다.
Random Forests에서 어떻게 동작하는지 보자, OOB 오류를 얻음.
library(randomForest)
rf = randomForest(X1, as.factor(Y1), xtest = X2, ytest = as.factor(Y2))
rf
# displays
Call:
randomForest(x = X1, y = as.factor(Y1), xtest = X2, ytest = as.factor(Y2))
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 4
OOB estimate of error rate: 24.11%
Confusion matrix:
bus opel saab van class.error
bus 91 1 1 2 0.04210526
opel 3 54 38 10 0.48571429
saab 5 31 64 9 0.41284404
van 0 1 1 112 0.01754386
Test set error rate: 26.48%
Confusion matrix:
bus opel saab van class.error
bus 119 0 0 4 0.03252033
opel 2 44 57 4 0.58878505
saab 4 31 63 10 0.41666667
van 0 0 0 85 0.00000000
과적합은 또한 발생되었다. 데이터에서 많은 중복으로 인해, 부트스트랩은 훌륭하게 동작하지 않는다 그리고, 아마도, 과적합이 원인 중 하나이다.
2 - 두번째 단계는 10-배 교차 검증을 포함한다. 아래에 결과를 보고한다. 모든 알고리즘은 GBM (ntree = 500, interaction.depth= 24, n.minobsinnode = 1, shrinkage = 0.05)을 제외하여 그들의 기본 인수(parameters)로 실행했다.
| Random Forests | ExtRa-Trees | GBM (optimized) | Random Uniform Forests | |
| Test error | 0.2518 (0.0535) | 0.2506 (0.0514) | 0.2234 (0.0422) | 0.2412 (0.0461) |
Table 1: 분류 (Vehicle Silhouette). n = 946, p = 18. 교차 검증 (10 folds). GBM을 제외한 튜닝 없음.
GBM은 잘 동작하지만 최적화 되어야 한다. 위의 검증 집합에서, 검증 오류는 0.2443에 유의. Random Uniform Forests는, 이 데이터셋에서 Random Forests 또는 Extra-Trees 보다 더 많은 차원을 사용하는 잘 정의된 기본 인수(parameters)를 가진 것처럼 보인다. 괄호 안에는 표준 편차를 보여준다.
5.1.3 German credit data (cost sensitive learning)
독일 신용 데이터(German credit)는 또 하나 잘 알려진 데이터셋이다. 저자의 말처럼, 데이터셋은 양호 혹은 불량 신용 위험의 속성 집합으로 묘사된다. 2가지 형식으로 제공된다(그들 모두 숫자). 또한 비용 매트릭스를 통해 제공. 우리는 100개 관측, 20개의 속성 그리고 2개의 구분(1: 양호 Good, 2: 불량 Bad)을 가지는 데이터의 숫자 형식을 사용한다.
독일 신용 데이터에서, 검증 에러는 비용 매트릭스(실제로는 불량인데 분류기의 예측이 양호이면 5, 양호일때 분류기의 예측이 불량이면 1)이기 때문에 적합하지 않다. 이런 까닭으로 비용을 최소화해야 한다. 이것을 달성하기위해, 우리는 AUC ( ROC 곡선 아래 영역) 그리고 AUPR (정밀-회수 곡선(precision-recall curve)아래 영역)을 최적화해야 한다. Fawcett (2006) 정의에 따라, AUC는 분류기가 부벙의 값보다 더 높은 임의()의 긍정 인스턴스('불량' 구분('Bad' class)) 순서를 매기는 확률이다. AUPR은 구분(class)가 실제로 하나인 경우에 긍정인 사례와 일치할 확률과 같다. 그러므로 신용 점수에 대해 두가지 모두 높을 필요가 있다.
- AUC는 긍정인 경우와 일치하는 신뢰 수준을 제공한다.
- AUPR은 긍정인 경우와 일치하기위해 수용 제한을 제공한다.
- AUC는 긍정인 경우와 일치하는 신뢰 수준을 제공한다.
- AUPR은 긍정인 경우와 일치하기위해 수용 제한을 제공한다.
비용 행렬이 제공되므로, 비용 민감 정확성(cost sensitive accuracy)은 실제 세계의 경우와 비슷하다. 이것은 혼돈 행렬과 포함 비용과 관계가 있다 그리고 독일 신용 데이터셋에서 다음을 가진다
n2, 1는 실제로는 ‘양호(Good)’(class 1)인 경우에 ‘불량(Bad)’(class 2)로 분류된 경우이다.
n1, 2는 실제로는 ‘Bad’인 경우에 ‘Good’로 분류된 경우이다.
n., 1는 ‘Good’인 경우의 전체 수이다
n.,2 는 ‘Bad’인 경우의 전체 수이다
n1, 2는 실제로는 ‘Bad’인 경우에 ‘Good’로 분류된 경우이다.
n., 1는 ‘Good’인 경우의 전체 수이다
n.,2 는 ‘Bad’인 경우의 전체 수이다
n1, 1과 n2, 2는 비용이 0이기 때문에 제외됨에 주의. 또한 다음으로 정의된 평균 비용(average
cost)을 사용한다
구분은 또한 균일하지 않다 그리고 구분 재가중 방법(class reweighting method) 또는 불균형한 분포(imbalanced distribution)에 무감각한 알고리즘은 없다, 이것은 어렵게 비용을 최소가 될 것이다. Random Uniform Forests는 Chen et Al. (2004)의 방법론을 약간 수정하여 사용하는 구분(class) 가중을 명시적으로 구현했다. 단순한 방법(각 구분(class)당 하나의 가중치)으로 구분 재가중치를 사용하는 방법인 SVM을 유일하게 찾았다, 우리는 비교를 위해 그것을 유지한다(Random Forests는 구분 가중 옵션(class weight option)을 가진다, 그러나 사용할 수 없는 것 같다).
여기에 우리가 사용하는 변수가 있다.
- Random Uniform Forests에서 classwt옵션은 각 구분(class)을 위한 비용 행렬을 반영하는 가중치를 사용한다. 최적화하지 않았고 그리고 구분 분포에 따라 그것을 설정했다. 만약 ‘Y’가 우리가 가지는 표기(label)의 R 벡터이면 e1071 R 패키지의 도움을 받았다:
# for SVM weights_svm = 100/table(Y) # Random Uniform Forests distribution = 100/table(Y) weights_ruf = round(distribution/min(distribution), 4)
SVM에서 다른 변수:
kernel = "sigmoid"
cost = 0.5.
kernel = "sigmoid"
cost = 0.5.
Random Uniform Forests에서, 약간의 표본 생성 기술을 사용했다:
- 각 노드에서 시도되는 특징 수를 위한 옵션. 이름 mtry = 3,
- 부트스트랩을 사용하지 않았고 그리고 기본값으로 하위-표본을 사용했다, subsamplerate = 0.7 그리고 replace = FALSE,
- 구분(class) 분포의 작은 부분(5%)를 교란했다(재가중하기 전), outputperturbationsampling = TRUE 그리고 oversampling = 0.05로 설정,
- forest를 안정시키기위해, 트리의 수 ntree = 500, 그리고 종료 노드 마다 최소 관측의 수 nodesize = 10 으로 설정
다른 옵션은 기본값으로 놓았다. 아래의 OOB 평가에서 매개 변수가 어떻게 사용하는지 방법을 찾을 수 있다.
먼저 데이터를 적재하고 그리고 단순히 교차-검증 스크립트를 실행한다(측정을 캡처하기위해 약간 수정). 재생산성을 위해, 같은 시드를 사용해야 한다.
germanCredit =
read.table("http://archive.ics.uci.edu/ml/machine-learning-databases/statlog/german/german.data-numeric")
XY = germanCredit
# set.seed(2014)
# separate Y and X and call a cross-validation procedure
# ...
아래에 결과가 있다:
| SVM | Random Uniform Forests | |
| Cost sensitive accuracy | 0.7492 (0.0553) | 0.7651 (0.0425) |
| Average cost | 0.551 (0.1297) | 0.517 (0.1) |
| AUC | 0.7333 (0.0550) | 0.6979 (0.0459) |
| AUPR | 0.6372 (0.0716) | 0.6451 (0.0661) |
| Test error | 0.283 (0.0605) | 0.385 (0.0479) |
구분(class) 가중 옵션을 사용하여 좋은 점수를 달성하는 두가지 방법, 좋은 비용 민감 정확성과 AUC 둘 모두를 얻는 중요한 요지. SVM은 고수준에서 주입한 후에 더 의존하는 동안, Random Uniform Forests는 ACPR(area under precision-recall curve)에 더 초점을 맞추고, 심지어 포인트를 얻기위해 테스트 오류를 증가시킨다. 좋은 점수에 도달하기위해, 최적화는 두가지 방법 모두에서 필요하다. 데이터셋이 가지는 특별한 문제 하나는 데이터에서 임의성이다 왜냐하면 많은 것이 범주형(2개 유일 값을 가짐)이기 때문. 그러므로, Random Uniform Forests는 차원에서 이득이 없다 그리고 다른 임의 기술(random techniques)은 정확성을 일정하게하기 위해 필요하다. 정형적으로 output perturbation sampling은 비용 민감 정확성(cost sensitive accuracy)이 0.74 한계를 넘도록 강요하는 것이 요지이다(그리고 평균 비용을 0.56 아래로 감소한다). 두가지 방법에서, 아마도 더 나은 점수에 도달할 수 있다.
OOB evaluation and the OOB classifier
그러면, 데이터셋을 평가하는데 유용한 OOB 평가와 우리가 사용한 약간의 도구를 보여준다.
# model and the OOB classifier
ruf.germanCredit = randomUniformForest(X, as.factor(Y), nodesize = 10,
mtry = 3, outputperturbationsampling = TRUE, oversampling = 0.05,
subsamplerate = 0.7, replace = FALSE, classwt = weights_ruf, ntree = 500)
ruf.germanCredit
# displays the OOB evaluation
#...
Out-of-bag (OOB) evaluation
OOB estimate of error rate: 37%
OOB error rate bound (with 1% deviation): 40.14%
OOB confusion matrix:
Reference
Prediction 1 2 class.error
1 370 40 0.0976
2 330 260 0.5593
OOB estimate of AUC: 0.6976
OOB estimate of AUPR: 0.6385
OOB estimate of F1-score: 0.5843
OOB geometric mean: 0.6768
#...
OOB cost sensitive accuracy는 0.7590이다 그리고 OOB average cost은 0.53이다. OOB 평가는 교차-검증 보다 더 비관적이다, 교차-검증은 전체 평가를 위해 데이터를 나눌 때 한번에 모든 데이터를 평가하기 때문이다. 그러므로 OOB 분석은 훈련(그리고 검증) 집합에 근접한다, 모델은 검증 집합이 제공되면 OOB 분류기가 일반화 되기 때문이다. 교차-검증 그리고 Random (Uniform) Forests에서, 그렇지는 않다.
위의 OOB 평가에서, 평균 비용을 줄이기 위해 검증 오류를 증가시키는데 필요한 방법을 볼 수 있다. 독일 신용 데이터셋에서 힘든 작업은 AUC를 줄이지 않으면서 높은 AUPR에 도달하는 것이다, 저렴한 비용의 핵심 요소인 민감도(sensitivity)와 정밀도(precision) 둘 모두 통제.
이 작업이 너무 쉽지 않은 이유를 보기 위해, 어떤 행렬의 시각화를 호출한다:
# get the ROC curve roc.curve(ruf.germanCredit, Y, unique(Y)) # get the Precision-Recall curve roc.curve(ruf.germanCredit, Y, unique(Y), falseDiscoveryRate = TRUE)
 |
| Figure 8: 독일 신용 데이터셋의 ROC와 Precision-Recall 곡선(OOB 평가) |
우리는 서로 다르게 보이는 두개의 플롯을 볼 수 있다(그러나 그것들은 구별이 안됨) 그리고 주요한 점은 각 그래프의 시작에 있다: 우리는 분명하게 어떤 경우(전체의 20% 까지)에서 관찰한다, 그들이 분류 'Bad'에서 온 것인지 아닌지 구별하기 힘들다 그리고 정밀도-회수(precision-recall)에서 더 분명하다: 정밀도는 너무 빨리 감소한다 그 결과 가중치는 다른 기술의 도움 없이 판별에 좋은 규칙을 관리하기에 충분하지 않다.
좋은 민감도((sensitivity), 회수(recall))는 보정 되지만 검증 오류는 나빠질 수 있다. 사실 임의 모델(randomized models)은 이 데이터셋에서 좋은 결과에 도달할 수 있을지라도, 그것은 약간의 불안정이 발생하게하는 것이 나타난다. 검증 오류가 트리의 수로 어떻게 감소되는지 볼 수 있다:
plot(ruf.germanCredit, ylim = c(0.25, 0.4))
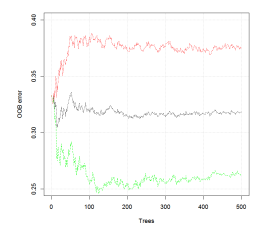
|
| Figure 9: 독일 신용 데이터셋에서 트리의 수에 따른 OOB 오류. |
오류 율은 트리의 수로 감소하지 않는다(혹은 약간 감소) 그리고 크게 불안정하다(빨강과 초록 선은 OOB가 놓일 수 있는 위치를 가리킨다, 검은 선은 그것의 실제 값을 추정한다). 결과적으로, 단일(혹은 약간)의 트리는 forest의 그것들과 더 근접한 결과를 얻는 것처럼 보인다. 사실, 이는 검증 오류에서만 적용된다. forest 분류기는 안정화 (위에서 분명히 않은) 보다 더 많은 것을 가져온다. 문제에 적응을 더 많이 한다. 5개서 10개의 트리의 forest를 비교, 500개의 트리의 앙상블은 AUC를 10% 넘게 그리고 AUPR를 30% 넘게 증가시키고, 그리고 검증 오류는 단지 5%만 감소한다.
5.1.4 Breast cancer data (more on Breiman’s bound)
우리는 Breiman 경계에 대해 약간의 말로 분류를 위한 평가를 매겼다. 다른 데이터 셋에서, 이것은 기대한 것 만큼 동작하지 않음에 유의해야 한다. 사실, 이것은 동작한다 그러나, 명백히, Breiman 경계는 최적의 분류기를 얻기 위해서 설계된 것이 아니라 강건한 분류기를 얻기 위해서이다. 예로, 독일 신용 데이터에서, mtry = 1로 놓으면(순수한 random forest를 얻음) Breiman 경계 아래에 OOB 오류가 있게 강제한다. 우리는 최적의 분류기를 얻는게 아니라, 아마도 더 강건한 하나를 얻기 위해서이다. 다른 말로, Breiman 경계는 대부분의 경우에 상단 경계에 있다 그러나 그것은 최적성(optimality)과 강건성(robustness) 간에 선택해야 한다. 3개의 요소가 필요하다:
- 충분한 데이터를 가져야 하고,
- 균형적인 분류, 그러나 실세계 문제는 일반적으로 불균형한 경우를 가진다,
- 공변량 사이에 낮은 상관관계.
- 균형적인 분류, 그러나 실세계 문제는 일반적으로 불균형한 경우를 가진다,
- 공변량 사이에 낮은 상관관계.
첫번째 조건은 행렬의 하나인 상관관계는 트리 간에 짝 경우를 찾기 위해 요구되므로 필요하다. 그러면, 500개의 관측으로 조차, 짝 OOB 경우는 그렇게 많지 않을 것이다 그리고 많은 상황에서 트리의 수는 변하지 않을 것이다. Random Uniform Forests는 불균형한 구분(class)에 민감하지 않다, 그러면 중요한 구분은(class)는 강한 영향을 가질 수 있다 (두번째 변수가 필요함).
상관관계가 있는 공변량은 과적합 위험을 증가시키는 경향이 있다, 그러면 상단 경계 유지는 쉽지가 않다, 그러므로, 모델의 기본 변수 변경은 Breiman 경계에 있게 하기 위해서 일반적으로 필요하다. 아래에서 그것이 어떻게 발생하는지 확인한다.
유방암 데이터셋(Breast cancer dataset)은 UCI 저장소에서 사용 가능하다. 아래의 링크에서 설명을 찾을 수 있다:
http://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic)
http://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic)
데이터 셋은 569개의 관측, 32개의 속성 그리고 2개의 구분을 가진다. 그러나 서식이 지정된 데이터에는 실제로 11 개의 특성이 있다.
# load the data
breastCancer =
read.table("http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",
sep = ",")
XY = breastCancer
# remove the first attribute which is a unique ID
XY = XY[,-1]
# get observations and labels (the 10th column)
Y = extractYFromData(XY, whichColForY = 10)$Y
X = extractYFromData(XY, whichColForY = 10)$X
여기서, 우리는 모든 모델에서 기본 변수를 사용했고 그리고 10-배 교차-검증 오류를 보여준다. 어떤 알고리즘은 R 매트릭스가 필요함에 주의, 다른 것들은 데이터 프레임이 필요하다 그리고 검증 오류는 데이터 프레임을 행렬로 변환하는 방법에 따라 아마도 영향이 있을 것이다.
| RF | ET | SVM | Random Uniform Forests | |
| Test error | 0.0314 (0.0161) | 0.03 (0.0124) | 0.0371 (0.0153) | 0.0314 (0.0175) |
Random Uniform Forests는 다른 것에 근접하고 그리고 이 데이터셋에서 많은 알고리즘이 통상 높은 정밀에 도달한다.
Breiman 경계를 확인하자. 공변량의 높은 상관관계와 구분(class)의 불균형 때문에 기본 변수를 사용하여 Breiman 경계에 일치하는 경우는 없다. 그러면 포인트를 얻기 위해, 우리는 output perturbation sampling (출력 섭동 표본) 옵션(oversampling으로 구분의 약 20%을 변경)을 사용했다, 트리 간에 상관관계를 증가시키고 강도(strength)를 약화되게 함. 그러면 우리는 노드 간에 더 많이 비교하도록 mtry를 64로 증가하고 그리고 forest를 안정화하기 위해 트리의 수를 500으로 설정한다. 모든 변수는 첫번째 훈련 표본으로만 설정했다 (데이터의 50%, 시작에 필요한 우리가 사용한 시드를 가짐). 그러면 우리는 5개의 임의 트리 그리고 검증 표본을 생성하고 그리고 OOB 오류를 확인한다, Breiman 경계과 검증 오류.
| OOB error | Breiman’s bound | Test error | |
| set 1 | 0.0315 | 0.0395 | 0.0315 |
| set 2 | 0.0287 | 0.0303 | 0.0257 |
| set 3 | 0.0401 | 0.0335 | 0.0257 |
| set 4 | 0.0372 | 0.0355 | 0.0286 |
| set 5 | 0.0287 | 0.0339 | 0.04 |
Breiman 경계는 현재 OOB 오류에 매우 가깝게 있다, 상관관계(correlation)와 강도(strength)에서 더 많은 가치가 있게 함. 전체 데이터에서 OOB 평가는 OOB 오류가 0.0372이 되게 하고 그리고 Breiman 경계는 0.0404가 되게 한다. 실세계의 경우에, Random Uniform Forests 는 일반화 오류에 너무 최적화 되지 않도록 진행하게 설계되었다.
5.2 Regression
회귀에서도, 우리는 수렴이 여전히 발생하는지 보기 위해 단지 약간의 경우에 output perturbation sampling 옵션을 추가하고 그들의 기본 변수를 가지고 Random Uniform Forest를 사용한다(첫번째 데이터셋에서 mtry제외). 또한 후-처리를 사용했다.
5.2.1 AutoMPG data
우리가 사용한 첫번째 데이터셋은 UCI 저장소에서 찾을 수 있는 autoMPG 이다. 설명: StatLib 라이브러에서 제공된 데이터 셋에서 약간 수정된 버전이다. 속성 “mpg” 예측에서 Ross Quinlan (1993)에 의해 사용되는 라인에서, 8개의 원본 인스턴스는 “mpg” 속성에서 알지 못하는 값을 가지기 때문에 제거되었다. 원본 데이터셋은 "auto-mpg.data-original" 파일에서 이용가능하다. 데이터는 398개의 관측과 8개의 속성을 가진다. 우리는 먼저 수정된 데이터를 얻고 10-배 교차 검증을 실행한다.
# load the data,
autoMPG = read.table("http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
XY = autoMPG
# remove the last column (car models) and get the mpg attribute (the first one)
XY = XY[,-9]
Y = extractYFromData(XY, whichColForY = 1)$Y
X = extractYFromData(XY, whichColForY = 1)$X
set.seed(2014)
우리는 범주형 데이터를 재정의했다, R 매트릭스로 데이터를 사용, 그렇지 않으면 입력된 데이터(데이터 프레임)가 가지는 어떤 오해와 알고리즘이 범주형 변수를 인식하는 방법 때문에 Rndom Forests(RF) algorithm 은 실행되지 않을 것이다. 하나의 변수는 실제로 범주형(마지막 하나, ‘origin’)이고 첫번째 하나(‘cylinders’)는 이산형(discrete)이다 그리고 정열될 수 있다.
또한 Random Forests의 가장 좋은 mtry를 찾기 위해 tuneRF() 함수를 사용한다. 최적값은 4이고 그리고 Extra Trees (ET)에서 그것을 사용한다.
SVM 은 비용 2.5 그리고 방사형 kernel (tune.svm() 함수로 평가)을 사용했다.
GBM (Gradient Boosting machines) 은 다른 데이터 셋에서 정의된 변수를 사용했다.
rUF 는 Random Uniform Forests를 나타내고 그리고 mtry 는 14로 설정되었다.
| RF | ET | SVM | GBM | rUF | rUF (post processing) |
|
| MSE | 7.46 (2.73) | 7.1 (2.71) | 7.31 (2.49) | 7.48 (2.69) | 7.15 (2.75) | 7.12 (2.76) |
Extremely Randomized Trees (ET)는 회귀에서 잘 동작한다, 그래서 우리는 Random Uniform Forest 에서 mtry 변수를 증가시킨 것이 더 나은 결과로 이끌지 않는지 궁금하다(ET는 단지 mtry = 4를 사용함). Random Uniform Forests에서 트리의 수를 100에서 200으로 증가함은 결과를 향상시키지 않는다. 그러나 ET는 더 많은 관측을 사용했고(전체 표본) Random Uniform Forest는 하위-표본(기본 수준(level) 0.7)을 사용했다. ET에서와 똑같은 변수를 사용하는 것은 MSE (약 7.13)가 변화하지 않도록 한다. 이 데이터셋에서, 하위-표본 또는 차원에서 더 많은 작업은 영향이 없는 것으로 보인다.
우리는 오류가 어떻게 보이는지 확인하기 위하여 그리고 miles per gallon (mpg) 변수가 다른 예측자를 어떻게 설명할 수 있는지 확인하기 위하여 전체 데이터셋(OOB 평가)을 지금 사용한다.
# run Random Uniform Forests
ruf.autompg = randomUniformForest(X,Y)
ruf.autompg
# displays
#...
Out-of-bag (OOB) evaluation
Mean of squared residuals: 7.1946
Mean squared error bound (experimental): 8.268037
Variance explained: 88.22%
OOB residuals:
Min 1Q Median Mean 3Q Max
-17.42000 -1.16500 0.27250 0.04214 1.43100 11.60000
Mean of absolute residuals: 1.84719
Breiman’s bounds
Theorical prediction error: 6.930812
Upper bound of prediction error: 7.023337
Mean prediction error of a tree: 15.13134
Average correlation between trees residuals: 0.4642
Expected squared bias (experimental): 0.000442
OOB 평가는 교차-검증에 근접한다. 설명된 변수의 비율이 높고 그리고 모델에서 신뢰를 가지게함을 확인한다. Random Uniform Forest는 목적을 이해하는데 사용할 수 있는 많은 다른 정보를 보여준다.
소비를 증가시키는 변수(그러므로 gallon 당 mile 감소)가 어떤 것인지 알기를 원한다고 가정하자. 우리는 partialImportance() 보다는 importance() 함수를 호출한다.
# importance
imp.ruf.autompg = importance(ruf.autompg, Xtest = X, maxInteractions = 7)
# which variables leads to consumption more than average
pImp.ruf.autompg = partialImportance(X, imp.ruf.autompg,
threshold = round(mean(Y),4),
thresholdDirection = "low")
소비의 증가에서 가장 중요하게 되는 변수’V5’(자동차의 무게) 그리고 ’V4’ (마력)를 얻는다. mpg가 이 2개의 변수를 어떻게 반영하는지 보자.
# Dependence between V5 and V4 and influence on the ’miles per gallon’
pDependence.V5V4 = partialDependenceBetweenPredictors(X, imp.ruf.autompg, c("V5", "V4"),
whichOrder = "all")
어떤 가치를 제공하는 플롯(그리고 변수의 상호작용 수준)을 얻는다:
 |
| Figure 10: 'V5' (무게)와 'V4' (마력) 간에 부분 의존도(Partial dependencies)
그리고 and 'gallon 당 miles(mpg)'에서 영향 (응답). |
mpg 의 높은 값은 낮은 무게와 높은 마력에 의존함을 볼 수 있다 그리고 (무게에서) 임계점이 교차할 때, 마력이 무엇이든 문제 없이 mpg는 감소한다. 무게와 마력 간에 의존도는 비-선형으로 보인다; 무게는 마력이 최소로 감소하는 동안 증가한다, 그러면 무게는 마력 역기 증가하는 동안 증가한다. 흥미로운 점은, 전체 관계에서, gallon 당 miles에 무엇이 발생하는지 알고 있다는 것이다.
5.2.2 Abalone, Concrete compressive strength, Boston housing data
우리는 3개의 데이터셋 평가로 회귀를 마친다(또한 UCI에서 이용 가능). 간결함을 위해, 우리는 여기서 R 코드를 사용하지 않는다 그리고 10-배 교차 검증 절차의 결과를 단순하게 보고한다. Random Uniform Forests는 기본 변수로 실행했다.
| RF | ET | SVM | GBM | rUF | rUF∗ | |
| Abalone | 4.59 (0.55) | - | 4.52 (0.54) | 4.88 (0.7) | 4.64 (0.54) | 4.74 (0.61) |
| Concrete | 23.05 (5.3) | 21.67 (5.38) | 34.55 (5.3) | 14.94 (3.95) | 21.64 (5.28) | 22.33 (5.82) |
| Housing | 10.19 (3.87) | 9.43 (3.69) | 11.23 (6.17) | 8.87 (5.73) | 9.32 (3.12) | 9.57 (4.57) |
Table 6: 회귀(전복(Abalone), 콘크리트 압축 강도(Concrete compressive strength) 그리고 보스턴 주택 데이터(Boston housing data) 집합). 10-배 교차-검증에서 평균 제곱 에러(mean squared error)와 표준 편차 보고. Random Uniform Forest를 제외한 모든 알고리즘 최적화.
*: 출력 섭동 표본(output perturbation sampling)(모든 훈련 과정은 random Gaussian 값으로 복제) 그리고 후-처리 수행.
*: 출력 섭동 표본(output perturbation sampling)(모든 훈련 과정은 random Gaussian 값으로 복제) 그리고 후-처리 수행.
가장 놀라운 사실은 예측 오류와 연결된다, 콘크리트 데이터셋에서, GBM은 다른 모두에 비해 너무 낮다. 확실하게 하기 위해 우리는 모델을 다시 실행했고 2-배 교차 검증으로 변경했다. 어떤 데이터 셋에서 GBM은 맞추기 힘들었다. Random Uniform Forest 에서 전체 표본의 사용은 MSE가 19.65를 가져 간격이 줄어든다.
그러나 요점은 무작위 가우시안 (random Gaussian)에 의한 훈련 응답의 값을 완전히 변경 한 후 사후 처리 (post-processing)를 수행 할 때, Random Uniform Forest는 그들의 표준인 경우에 근접한다. 게다가, 결과의 섭동(perturbation of the output)은 Random Forest 보다 나쁜 결과로 이끌지 않는다. 회귀에서, 최적의 분할-점을 선택하지 않으므로 더 효과적으로 보인다는 것이다, 이는 Extremely Randomized Trees와 Random Uniform Forests의 예측 오류는 Breiman’s Random Forests 에서 보다 낮거나 또는 비슷하게 되는 경향과 같다.


댓글 없음:
댓글 쓰기