개요(Abstract)
인공 신경망은 많은 상황에서 적용된다. neuralnet은 회귀 분석의 문맥에서 다-층 퍼셉트론(multi-layer perceptrons)을 생성한다, i.e., 공변량(covariates)과 응답 변수 간에 함수 관계를 근사화. 그러므로, 신경망은 일반화 선형 모델의 확장으로 사용된다.
neuralnet은 유연한 패키지이다, 역전파(backpropagation) 알고리즘 그리고 탄력적인 역전파(resilient backpropagation)의 3개의 버전이 구현되었고 그리고 그것은 활성화(activation) 그리고 에러 함수(error function)의 사용자-선택을 제공한다. 공변량과 응답 변수의 임의의 수 뿐만 아니라 숨김 층(hidden layers)은 이론적으로 포함될 수 있다.
논문은 다층 퍼섭트론 그리고 탄력적 역전파의 간략한 소개를 제공하고 그리고 테이터 셋 infert 사용하는 neuralnet의 응용을 설명한다, R 배포에 포함.
원본 : PDF
출처 : R JOURNAL
소개(Introduction)
많은 상황에서, 공변량(또한 입력 변수로 알려짐) 그리고 응답 변수(또한 출력 변수로 알려짐) 간에 함수적 관계에 큰 관심을 가진다. 예를 들어 복잡한 질병을 모델링 할 때, 질병에서 잠재 위험 요소 그리고 그들의 영향은 예방 또는 개입 전략을 개발하기 위해 사용될 수 있는 그들의 위험 요소를 구별하기 위해 연구된다. 일반화 선형 모델과 달리(generalized linear models, GLM, McCullagh and Nelder, 1983), 그것은 선형 조합의 예에서 처럼 공변량과 응답 변수 간의 관계 타입을 사전에 명시할 필요가 없다. 이것은 인공 신경망을 가치있는 통계적 도구로 만든다. 그들은 특히 GLM의 직접적인 확장이다 그리고 비슷한 방법으로 적용된다. 관측 데이터는 신경망 훈련에 사용되고 그리고 신경망은 그것의 변수를 반복적용하여 근사적인 관계를 학습한다.
패키지 neuralnet (Fritsch and Günther, 2008)은 feed-forward 신경망 훈련을 위한 매우 유연한 함수를 가진다, i.e., 위 상황에서 함수적 관계를 근사화하기 위해. 그것은 이론적으로 공변량 그리고 응답변수 뿐만 아니라 hidden layers 그리고 hidden neurons의 임의의 수를 처리할 수 있다 비록 계산 비용은 복잡도 순서로 지수적로 증가할 수 있지만. 이것은 반복 진행을 쉽게 멈출수 있게 한다 그러므로 최대 반복 단계 수, 사용자에 의해 정의될 수 있음, 알고리즘 수렴 전에 도달된다. 게다가, 패키지는 결과를 시각화하는 함수를 제공한다 또는 일반적으로 신경망 사용을 편리하게 하기 위함. 예를 들어 함수 compute는 새로운 공변량 조합에서 예측을 계산하기 위해 적용할 수 있다.
지금 인공 신경망을 처리하는 다른 2개의 패키지가 있다: nnet (Venables and Ripley, 2002) 그리고 AMORE (Limas et al., 2007). nnet은 전통적인 역전파를 가지고 feed-forward 신경망을 훈련 기회를 제공한다, 그리고 AMORE 에서, TAO 강건한 신경망(TAO robust neural network) 알고리즘이 구현되었다. neuralnet은 회귀 분석의 맥락에서 신경망을 훈련하기 위해 만들어 졌다. 그러므로, 탄력적 역전파(backpropagation)가 사용되었고 그러므로 이 알고리즘은 이 목적에서 가장 빠른 알고리즘의 하나 이다 (e.g. Schiffmann et al., 1994; Rocha et al., 2003; Kumar and Zhang, 2006; Almeida et al., 2010). 3개의 다른 버전이 구현되었고 그리고 전통적인 역전파는 비교 목적으로 포함되었다. 활성화 및 에러 함수를 사용자가 선택함으로, 패키지는 매우 유연하다. 사용자는 몇 개의 숨김 층(hidden layers) 사용이 가능하다, 여분의 숨김 층을 포함하여 계산 비용을 줄일 수 있음. 우리는 성공적으로 이 패키지를 복잡한 질병 모델 생성에 사용했다, i.e., 생물 유전자 - 유전자 상호 작용(biological gene-gene interactions)의 다른 구조(Günther et al., 2009). 요약, neuralnet은 R에서 신경망을 훈련하기 위해 제공된 알고리즘과 관계되는 틈을 닫았다.
인공 신경망의 새로운 사용자를 위해 패키지 사용이 쉽도록, neuralnet에서 구현된 신경망과 학습 알고리즘의 간략한 소개는 그것의 어플리케이션 설명 전에 주어진다.
다층 퍼셉트론 (Multi-layer perceptrons)
패키지 neuralnet은 다층 퍼셉트론(multi-layer perceptrons)에 초점을 맞췄다(MLP, Bishop, 1995), 함수적 관계 모델을 구축할 때 잘 응용할 수 있음. MLP의 하부 구조는 방향성 그래프(directed graph)이다, i.e. 그것은 정점과 방향을 가진 간선으로 구성된다, 이 문맥에서는 뉴런(neurons) 그리고 시냅스(synapses)로 불림. 뉴런은 층(layers)에서 조직화된다, 보통은 시냅스로 완전하게 연결됨. neuralnet에서, 시냅스는 오로지 연속적인(인접한) 층을 연결한다. 입력 층은 분리된 뉴런에서 모든 공변량(covariates)으로 구성된다 그리고 출력 층은 응답 변수로 구성된다. 그것들 사이에 있는 층은 숨김 층(hidden layers)으로 언급된다, 그들을 직접 관찰할 수 없으므로. 입력 층과 숨김 층은 시냅스 교차에 연관하는 불변 뉴런을 포함한다, i.e. 시냅스는 어떤 공변량에 의해 직접적으로 영향을 받지 않는다. Figure 1은 3개의 숨김 뉴런으로 구성된 하나의 숨김 층을 가지는 신경망의 예이다. 신경망은 2개의 변수 A 그리고 B 그리고 응답 변수 Y 간에 관계의 모델이다. neuralnet은 이론적으로 공변량의 응답 변수에 대한 임의의 수의 포함하도록 허용한다. 어쨌든, 공변량 그리고 응답 변수 둘 모두 거대한 수를 사용하는 융합의 어려움이 발생할 수 있다.
 |
Figure 1: 2개의 입력 뉴런(A 그리고 B), 하나의 출력 뉴련(Y) 그리고 3개의 숨김 뉴런으로 구성된 하나의 숨김 층을 가지는 신경망의 예. |
시냅스 각각에서, 가중치는 상응하는 뉴런에 영향을 나타내게 붙여졌다, 그리고 모든 데이터는 신호(signal)로 신경망에 전달된다. 신호는 모든 들어오는 신호를 묶은 이른바 통합 함수에서 첫번째로 진행한다 그리고 뉴런의 출력을 변경하는 이른바 활성화 함수가 두번째.
가장 단순한 다층 퍼셉트론(또한 퍼셉트론으로 알려짐)은 n개의 공변량의 입력 층 그리고 하나의 출력 뉴런을 가지능 출력 층으로 구성된다.
그것의 계산 함수:

ω0는 교차점(intercept)를 나타냄, w = (ω1, ... , ωn) 벡터는 교차점이 없는 모든 시냅스 가중치로 구성, 그리고 x = (x1, ... , xn) 벡터는 모든 공변량으로 구성. 함수는 링크 함수 ƒ-1를 가지는 GLM과 수학적으로 동등하다. 그러므로, 모두 계산된 가중치는 이 경우에서 GLM의 회귀 변수와 같다.
모델 생성을 유연하게 하기 위해, 숨김 층이 포함되었다. 어쨌든, 호르닉(Hornik et al. (1989))은 하나의 숨김 층은 어떤 구분 연속 함수(any piecewise continuous function)의 모델을 구축함에 충분하다고 보여 주었다. J 개의 숨김 뉴런으로 구성된 숨김 층을 가지는 MLP 처럼 아래의 함수로 계산한다:
ω0는 출력 뉴런의 교차점을 나타내고 그리고 ω0j는 j번째 숨김 뉴런의 교차점. 추가적으로, ωj는 j번째 숨김 뉴런에서 시작하는 시냅스에 상응하는 시냅스 가중치를 나타낸다 그리고 출력 뉴런으로 이끈다, wj = (ω1j, ... , ωnj)는 j번째 숨김 뉴런으로 이끄는 시냅스에 상응하는 모든 시냅스 가중치의 벡터, 그리고 x = (x1, ... , xn)는 모든 공변량 벡터. 이것은 신경망이 GLM에서 직접적인 확장임을 보여준다. 어쨌든, 변수, i.e 가중치, 더 이상 같은 방법으로 해석하지 않을 것이다.
공식적인 언급, 모든 숨김 뉴런과 출력 뉴런은 모든 진행 뉴런 z0, z1, ..., zk의 출력으로 부터 출력 ƒ(g(z0, z1, ..., zk)) = ƒ(g(z))를 계산한다, g:Rk+1 → R 는 통합 함수를 표시하고 그리고 ƒ:R → R 은 활성화 함수인 경우. 뉴런 z0 ≡ 0 은 교차점에 속해 있는 상수 1 이다. 통합 함수는 종종
g(z) = ω0z0 + Σi = 1k ωizi = ω0 + wTz
으로 정의된다. 활성화 함수 ƒ는 일반적으로 경계가 있고 감소하지 않는 비선형이다 그리고 로지스틱 함수 (ƒ(μ) = 1 / (1 + e-μ)) 또는 쌍곡선 탄젠트(the hyperbolic tangent) 같은 미분 함수(differentiable function). 그것은 GLM에서의 경우와 마찬가지로 응답 변수에 관계로 선택될 것이다. 로지스틱 함수는, 예를 들어, 이진 응답 변수에 적당하므로 그것은 구간 [0, 1]에서 각 뉴런의 출력과 일치한다. 이 순간, neuralnet은 모든 뉴런에서 같은 통합 뿐만 아니라 활성화 함수를 사용한다 .
감독 학습 (Supervised learning)
신경망은 훈련 과정 동안 학습 알고리즘에 의해 데이터를 적합한다. neuralnet는 감독 학습 알고리즘(supervised learning algorithms)에 초점을 맞췄다. 이런 학습 알고지즘은 예측된 출력과 비교하는 주어진 입력의 사용 그리고 이 비교에 따라 모든 변수의 적응으로 특징지어 진다. 신경망의 변수는 그것의 가중치이다. 모든 가중치는 표준 정규 분포에서 나오는 무작위 값을 가지고 일반적으로 초기화된다. 훈련 과정의 반복 동안, 아래의 단계가 반복된다:
- 신경망은 주어진 입력 x와 현재 가중치로 출력 o(x)를 계산한다. 만약 훈련 과정이 아직 끝나자 않았다면, 예측된 출력 o는 관측된 값 y와 다를 것이다.
-
에러 함수 E, 제곱 에러의 합(sum of squared errors (SSE))과 같음
E = (1/2) ΣLl=1ΣHh=1(olh - ylh)2혹은 교차 엔트로피E = − ΣLl=1ΣHh=1(ylhlog(olh) + (1 − ylh)log(1 − olh))예측과 관측된 출력의 차이를 측정, l = 1, ... , L 은 관측의 수 이디ㅏ, i.e. 주어진 입력-출력 쌍, 그리고 h = 1, ... , H 는 출력 노드이다.
- 모든 가중치는 학습 알고리즘의 규칙에 따라 적용된다.
과정은 만약 미리-정의된 기준을 만족하면 중지된다, e.g. 만약 가중치 (∂E/∂ω)으로 기대값을 가지는 에러 함수의 모든 절대 편도 함수(absolute partial derivatives)가 주어진 임계치 보다 작다면. 다양하게 사용되는 학습 알고리즘은 탄력적 역전파(resilient backpropagation) 알고리즘이다.
역전파 및 탄력적 역전파 (Backpropagation and resilient backpropag)
탄력적 역전파 알고리즘은 지역 최대 에러 함수(local minimum of the error function)를 찾기 위해 신경망 가중치를 수정한 전통적인 역전파 알고리즘에 기반한다. 그러므로 에러 함수 (∂E/∂w)의 기울기는 근을 찾기 위한 가충치에 대해 계산한다. 특히, 가중치는 지역 최소값에 다달을 때까지 편미분(partial derivatives)의 반대 방향으로 진행하도록 수정했다. 이 기본 개념은 단변량(univariate) 에러-함수에서 Figure 2에 개략적으로 설명했다.
 |
Figure 2: 단변량 에러 함수 E(ω)로 설명하는 역전파 알고리즘의 기본 개념. |
만약 편미분(partial derivative)이 음수이면, 가중치는 증가된다(그림의 왼쪽); 만약 편미분이 양수이면, 가중치는 감소된다(그림의 오른쪽). 모든 편미분은 신경망에 계산되는 함수를 기본적으로 통합 그리고 활성화 함수이므로 chain rule을 이용하여 계산된다. 상세한 설명은 Rojas (1996)에 주어진다.
neuralnet은 역전파 간에 변경할 기회를 제공한다: (Riedmiller, 1994)를 가지는 탄력적 역전파 또는 가중치 역전파가 없는 탄력적 역전파 (Riedmiller and Braun, 1993) 그리고 Anastasiadis et al. (2005)에 의해 수정된 전역 수렴 버전. 모든 알고리즘은 가중치가 기울기의 반대 방향으로 가도록 학습 비를 추가함으로써 에러 함수를 최소화 하기 위해 노력한다.
전통적 역전파 알고리즘과 달리, 분할 학습 비 ηk, 훈련 과정에서 변경, 각 탄력적 역전파에서 사용된다. 이것은 전체 훈련 과정 그리고 전체 망에 적당한 전체-모든 학습 비 정의 문제를 해결한다. 추가적으로, 편미분의 크기 대신에 오로지 그들의 부호는 가중치를 갱신하기 위해 사용한다. 이것은 전체 망에서 학습 비의 동등한 영향을 보장한다(Riedmiller and Braun, 1993). 가중치는 아래의 규칙으로 조정된다:
, 반대로는
전통적인 역전파에서, t는 반복 단계를 나타내고 그리고 k는 가중치.
얕은 지역에서 수렴(convergence) 속도를 빠르게 하기 위해, 학습 비 ηk는 증가할 것이다 만약 편미분에 상응하는 그것의 부호가 같다면. 반대로, 그것은 감소할 것이다 만약 에러 함수의 편미분의 부호가 변경된다면, 부호 변경은 최소값을 너무 큰 학습 비 때문에 노쳤다고 가리키므로. 가중치 역추적은 다음 단계에서 마지막 반복을 취소하고 그리고 더 작은 값을 추가하는 기술이다, 알고리즘음 최소 몇 회에서 건너 뛸 수 있다. 예를 들어 가중치 역추적(weight backtracking)을 가지는 탄력적인 역전파 의사 코드(pseudocode)는 다음으로 주어진다(Riedmiller and
Braun, 1993):
for all weights{
if (grad.old*grad>0){
delta := min(delta*eta.plus, delta.max)
weights := weights - sign(grad)*delta
grad.old := grad
}
else if (grad.old*grad<0){
weights := weights + sign(grad.old)*delta
delta := max(delta*eta.minus, delta.min)
grad.old := 0
}
else if (grad.old*grad=0){
weights := weights - sign(grad)*delta
grad.old := grad
}
}
일반 역전파는 다음으로 주어지는 경우
for all weights{
weights := weights - grad*delta
}
Anastasiadis et al. (2005)이 소개한 전역 수렴 버전(globally convergent version)은 모든 다른 학습 비와 관계하여 하나의 학습 비의 추가적인 수정을 가지는 탄력적 역전파를 수행한다. 그것은 최소 절대 편미분을 연계한 학습 비 이거나 가장 작은 학습 비(i를 가지는 색인) 이다, 이것은 다음 식에 따라 변경된다:
만약
 그리고 0 ⟨ δ ⟨⟨ ∞ 이면. 더 상세한 내용은 Anastasiadis et al. (2005)를 보라.
그리고 0 ⟨ δ ⟨⟨ ∞ 이면. 더 상세한 내용은 Anastasiadis et al. (2005)를 보라.
 그리고 0 ⟨ δ ⟨⟨ ∞ 이면. 더 상세한 내용은 Anastasiadis et al. (2005)를 보라.
그리고 0 ⟨ δ ⟨⟨ ∞ 이면. 더 상세한 내용은 Anastasiadis et al. (2005)를 보라.
Using neuralnet
neuralnet은 2개의 다른 패키지에 의존한다: grid 그리고 MASS (Venables and Ripley, 2002). 그것의 사용은 lm 그리고 glm 같은 회귀 분석을 처리하는 함수에 기댄다. 필수 인수로, response variables ˜ sum of covariates 의 조건에서 식 그리고 공변량을 가지는 데이터 셋 그리고 응답 변수가 지정되어야 한다. 기본 값은 모든 다른 변수에 정의되었다 (다음 하위 절을 보라 ). 우리는 그것의 어플리케이션을 설명하기 위해 패키지 datasets에서 제공되는 데이터 셋 infert를 사용한다. 이 데이터 세트는 자연(spontaneous)과 인공 유산( induced abortion) 후 불임(infertility)을 조사한 환자 - 대조군 연구(case-control study)의 데이터가 포함되어 있습니다(Trichopoulos et al., 1976). 데이터 셋은 248개의 관측, 83명의 불임 여성 그리고 165명의 불임이 아닌 여성. 그것은 다른 변수들 사이에 포함되었다: age, parity, induced, 그리고 spontaneous. 변수 induced 그리고 spontaneous는 이전에 인공 및 자연 유사의 수를 나타낸다, 각각. 두 변수는 가능 값 0, 1을 가진다 그리고 2는 0, 1 관계함 그리고 2 또는 더 많은 이전 유산 경험. 년으로 나이는 변수 age에 주어진다 그리고 parity에 출산 횟수.
신경망 훈련 (Training of neural networks)
신경망 훈련을 위해 사용하는 함수 neuralnet은 필요한 복잡도에 따라 숨김 층(hidden layers)과 숨김 뉴런(hidden neurons)의 요구되는 수를 정의할 기회를 제공한다. 계산 함수의 복잡도는 숨김 층 또는 숨김 뉴런으로 증가한다. 기본 값은 하나의 숨김 뉴런을 가지는 하나의 숨김 층이다. 함수에서 가장 중요한 인수는 계속 설명:
- formula, 적합되는 모델의 기호 설명(위를 보라). 기본값 없음
- data, formula로 지정된 변수를 가지는 데이터 프레임. 기본값 없음
- hidden, 각 층에서 숨김 층과 숨김 뉴런의 수를 지정하는 벡터. 예로 벡터 (3, 2, 1)은 3개의 숨김 층을 나타낸다, 3개는 첫번째 층, 2개를 가지는 2번째 그리고 1개의 숨김 뉴런을 가지는 세번째. 기본값: 1
- threshold, 중단 기준으로 에러 함수의 편미분(partial derivatives)을 위한 임계값을 지정하는 숫자. 기본값: 0.01.
- rep, 훈련 과정의 반복 수. 기본값 1.
- startweights, 가중치에 대한 시작 값으로 지정된 값을 가지는 벡터. 기본: 표준 정규 분포의 무작위 수
- algorithm, 알고리즘 타입을 가지는 스트링. 가능한 값은 "backprop", "rprop+", "rprop-", "sag", 또는 "slr" 이다. "backprop"은 전통적인 역전파(backpropagation)를 언급한다. "rprop+" 그리고 "rprop-"는 가중치를 가지거나 가지지 않는 탄력적 연전파(resilient backpropagation)를 언급한다 그리고 "sag" 와 "slr"는 수정 전역 수렴 알고리즘(modified globally convergent algorithm)을 언급한다(grprop). "sag" 와 "slr"는 모든 다른 것에 따라 변경되는 학습 비를 정의한다. "sag"는 가장 작은 절대 편차(the smallest absolute derivative)를 언급한다, "slr"는 가장 작은 학습 비(the smallest learning rate). 기본값: "rprop+"
- err.fct, 미분 오차 함수(a differentiable error function). 문자열 "sse" 그리고 "ce"를 사용할 수 있다, '제곱합 에러(sum of squared errors)' 그리고 '교차 엔트로피(cross entropy)'. 기본값 "sse"
- act.fct, 미분 활성화 함수(differentiable activation function). 로지스틱 함수(logistic function) 그리고 탄젠트 쌍곡선(tangent hyperbolicus)을 위한 문자열로 "logistic" 그리고 "tanh"이 가능하다. 기본값 "logistic"
- linear.output, 논리값. act.fct가 출력 뉴런에 적용되지 않는다면, linear.output는 TRUE 이여야 한다. 기본값: TRUE
- likelihood, 논리값. 만약 에러 함수가 음의 로그-우도 함수가 아니면, likelihood는 TRUE 이여야 한다. 아카이케 정보 함수(Akaike’s Information Criterion: AIC, Akaike, 1973) 그리고 베이즈 정보 함수(Bayes Information Criterion: BIC, Schwarz, 1978)가 그러면 계산된다. 기본값 FALSE
- exclude, 훈련에서 배제되는 가중치를 지정하는 벡터 또는 메트릭. n개의 행과 3개의 열을 가지는 메트릭은 n개 가중치를 배제한다, 첫번째 열은 층(layer), 두번째 열은 가중치의 입력 뉴런, 그리고 세번째 가중치의 출력 뉴런. 만약 벡터로 주어지면, 정확한 개수가 알려져야 한다. 개수는 제공된 플롯 또는 저장된 시작 가중치를 사용하여 검증될 수 있다. 기본값: NULL
- constant.weights, 고정된 훈련 또는 처리에서 배제될 가중치의 값을 지정하는 벡터. 기본값: NULL
neuralnet의 사용은 응답 변수로 환자-대조군 상태(case)와 age, parity, induced 그리고 spontaneous의 공변량 간의 관계 모델 생성을 설명한다. 응답 변수는 이진이므로, 활성화 함수는 로지스틱 함수(기본) 그리고 교차-엔트로피(cross-entropy (err.fct="ce"))를 선택할 수 있다. 추가적으로, 항목 linear.output은 출력이 구간 [0, 1]의 활성화 함수에 일치되도록 보장하기 위하여 FALSE로 정할 수 있다. 숨김 뉴런의 수는 필요한 복잡도 관계에서 정할 수 있다. 2개의 숨김 뉴런을 가지는 신경망은 아래 문장으로 훈련된다.
> library(neuralnet)
Loading required package: grid
Loading required package: MASS
>
> nn <- neuralnet(
+ case~age+parity+induced+spontaneous,
+ data=infert, hidden=2, err.fct="ce",
+ linear.output=FALSE)
> nn
Call:
neuralnet(
formula = case~age+parity+induced+spontaneous,
data = infert, hidden = 2, err.fct = "ce",
linear.output = FALSE)
1 repetition was calculated.
Error Reached Threshold Steps
1 125.2126851 0.008779243419 5254
훈련 과정과 훈련된 신경망에 대한 기본 정보는 nn에 저장되었다. 이것은 시작 가중치의 예와 마찬가지로 결과를 재현하기 위해 알아야만 하는 모든 정보가 포함된다.
- net.result, 전체 결과를 가지는 목록, i.e. 출력, 각 응답(replication)에서 신경망.
- weights, 각 응답(replication)에서 신경망의 적합된 가중치를 가지는 목록.
- generalized.weights, 각 응답(replication)에서 신경망의 일반화 가중치를 가지는 목록
- result.matrix, 에러를 가지는 메트릭, 도달한 임계점, 필요한 단계, AIC 그리고 BIC (likelihood=TRUE인 경우 계산) 그리고 각 응답(replication)에서 추정 가중치. 각 열은 하나의 응답(replication)를 나타낸다.
- startweights, 각 응답(replication)에서 시작 가중치를 가지는 목록.
주요 결과의 요약은 nn$result.matrix에서 제공된다:
> nn$result.matrix
1
error 125.212685099732
reached.threshold 0.008779243419
steps 5254.000000000000
Intercept.to.1layhid1 5.593787533788
age.to.1layhid1 -0.117576380283
parity.to.1layhid1 1.765945780047
induced.to.1layhid1 -2.200113693672
spontaneous.to.1layhid1 -3.369491912508
Intercept.to.1layhid2 1.060701883258
age.to.1layhid2 2.925601414213
parity.to.1layhid2 0.259809664488
induced.to.1layhid2 -0.120043540527
spontaneous.to.1layhid2 -0.033475146593
Intercept.to.case 0.722297491596
1layhid.1.to.case -5.141324077052
1layhid.2.to.case 2.623245311046
에러 함수의 모든 절대 편미분이 0.01 보다 작게 될 때까지 훈련 과정은 5254 단계가 필요하다(기본 임계치). 추정 가중치의 범위는 −5.14 에서 5.59 까지이다. 예를 들어, 첫번째 숨김 층의 교차점은 5.59와 1.06 이다 그리고 첫번째 숨김 뉴런으로 이끄는 4개의 가중치는 공변량 age, parity, induced 그리고 spontaneous 각각에서 −0.12, 1.77, −2.20, 그리고 −3.37으로 추정된다. 만약 에러 함수가 음의 로그-우도 함수와 같다면, 에러는 아카이케 정보 기준(Akaike’s Information Criterion (AIC))로 계산되는 우도를 언급한다.
주어진 데이터는 nn$covariate 그리고 nn$response 뿐만 아니라 사용하지 않은 변수를 가지는 전체 데이터를 위한 nn$data에 저장된다. 신경망 출력은, i.e. 적합 값 o(x), nn$net.result로 제공된다.
> out <- cbind(nn$covariate,
+ nn$net.result[[1]])
> dimnames(out) <- list(NULL,
+ c("age","parity","induced",
+ "spontaneous","nn-output"))
> head(out)
age parity induced spontaneous nn-output
[1,] 26 6 1 2 0.1519579877
[2,] 42 1 1 0 0.6204480608
[3,] 39 6 2 0 0.1428325816
[4,] 34 4 2 0 0.1513351888
[5,] 35 3 1 1 0.3516163154
[6,] 36 4 2 1 0.4904344475
이 경우에, 객체 nn$net.result는 하나의 계산된 응답(replication)에 연관된 단지 하나의 요소로 구성되는 목록이다. 만악 하나의 응답(replication) 보다 더 많다면, 출력은 분리된 요소에 각각 저장될 것이다. 이 접근은 각 응답(replication)에서 하나의 행을 가지는 메트릭으로 저장되는 net.result와는 별개로 응답(replication)에 의해 변경되는 모든 값에서 같다.
이 결과를 비교하기 위해, 신경망을 algorithm="backprop"와 패키지 nnet을 가지고 위의 neuralnet처럼 설정된 같은 변수를 가지고 훈련한다.
> nn.bp <- neuralnet(
+ case~age+parity+induced+spontaneous,
+ data=infert, hidden=2, err.fct="ce",
+ linear.output=FALSE,
+ algorithm="backprop",
+ learningrate=0.01)
> nn.bp
Call:
neuralnet(
formula = case~age+parity+induced+spontaneous,
data = infert, hidden = 2, learningrate = 0.01,
algorithm = "backprop", err.fct = "ce",
linear.output = FALSE)
1 repetition was calculated.
Error Reached Threshold Steps
1 158.085556 0.008087314995 4
>
>
> nn.nnet <- nnet(
+ case~age+parity+induced+spontaneous,
+ data=infert, size=2, entropy=T,
+ abstol=0.01)
# weights: 13
initial value 158.121035
final value 158.085463
converged
nn.bp 과 nn.nnet는 같은 결과를 보인다. 둘 모두 훈련 과정은 마지막 매우 적은 반복 단계 그리고 에러는 거의 158이다. 그러므로 이 작은 비교에서, 모델 적합은 탄력적 역전파로 도달한 것 보다 덜 만족스럽다.
neuralnet은 "Intrator and Intrator (2001)"으로 소개된 일반화 가중치의 계산을 포함한다. 일반화 가중치 ωi는 i번째 공변량의 기여도를 로그-승산(log-odds)으로 정의된다:.
일반화 가중치는 각 공변량 xi의 영향을 표현한다 따라서 회귀 모델에서 i번째 회귀 변수의 유사한 해석(analogous interpretation)을 가진다. 어쨌든, 일반화 가중치는 모든 공변량에 의존한다. 그것의 기여도는 공변량의 영향이 선형인지 아닌지 가리킨다 그러므로 작은 변화는 선형의 효과로 추정한다 (Intrator and Intrator, 2001). 그들은 nn$generalized.weights에 저장되고 아래의 포멧으로 제공된다(반올림된 값)
> head(nn$generalized.weights[[1]])
[,1] [,2] [,3] [,4]
1 0.0088556 -0.1330079 0.1657087 0.2537842
2 0.1492874 -2.2422321 2.7934978 4.2782645
3 0.0004489 -0.0067430 0.0084008 0.0128660
4 0.0083028 -0.1247051 0.1553646 0.2379421
5 0.1071413 -1.6092161 2.0048511 3.0704457
6 0.1360035 -2.0427123 2.5449249 3.8975730
열은 4개의 공변량 age (j = 1), parity (j = 2), induced (j = 3), 그리고 spontaneous (j = 4)를 언급한다 그리고 일반화 가중치는 각 관측에서 주어진다 비록 그들은 각 공변량 조합과 같지만.
결과의 시각화 (Visualizing the results)
훈련 과정의 결과는 2개의 다른 플롯으로 시각화할 수 있다. 첫째로 훈련된 신경망은 단순히 아래 명령으로 그릴 수 있다.
> plot(nn)
결과 그림은 Figure 3에 주어졌다.
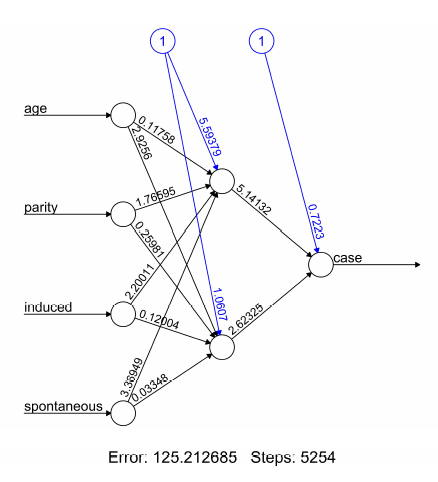 |
Figure 3: 훈련 과정에 대한 훈련된 시냅스 가중치와 기본 정보를 포함하는 훈련된 신경망의 플롯. |
이것은 훈련된 신경망의 구조를 반영한다, i.e. 망 위상(network topology). 그림은 기본 훈련된 시냅스 가중치, 모든 교차점 뿐만 아니라 전체 에러 그리고 수렴에 필요한 반복 수 같은 훈련 과정을 포함한다. 특히 큰 신경망을 우해, 그림과 각 뉴런의 크기는 변수 dimension 그리고 radius 각각을 사용하여 결정할 수 있다.
결과를 시각화하는 3번째 가능한 방법은 일반화 가중치를 그리는 것이다. gwplot는 nn$generalized.weights에서 제공되는 계산된 일반화 가중치를 사용한다 그리고 아래의 구문으로 사용할 수 있다.
> par(mfrow=c(2,2)) > gwplot(nn,selected.covariate="age", + min=-2.5, max=5) > gwplot(nn,selected.covariate="parity", + min=-2.5, max=5) > gwplot(nn,selected.covariate="induced", + min=-2.5, max=5) > gwplot(nn,selected.covariate="spontaneous", + min=-2.5, max=5)
상응하는 그림은 Figure 4에서 보여진다.
 |
Figure 4: 각 공변량에 관하여 일반화 가중치의 그림. |
일반화 가중치는 같은 범위 안에서 모든 공변량에서 주어진다. 일반화 가중치의 기여는 공변량 age는 환자-대조군 상태에 영향이 없다고 추정한다 그러므로 모든 일반화 가중치는 거의 0 이다 그리고 적어도 2개의 공변량 induced 과 spontaneous는 비-선형 영향을 가진다 그러므로 그들의 일반화 가중치 분산은 전체에서 1 보다 더 크다.
추가 특징 (Additional features)
compute 함수 (The compute function)
compute는 각 뉴런의 결과를 계산하고 요약한다, i.e. 입력, 감춰진 모든 뉴런 그리고 출력 층. 그러므로, 그것은 주어진 공변량 조합으로 신경망에 모든 신호 전달을 추적하기 위해 사용할 수 있다. 이것은 훈련된 신경 망의 망 위상을 해석하는데 도움을 준다. 그것은 또한 새로운 공변량 조합에서 예측을 계산하기 위해 쉽게 사용 가능하다. 신경망은 알려진 입력-출력 쌍으로 구성되는 훈련 데이터 집합을 가지고 훈련된다. 그것은 입력과 출력 간의 관계의 근사도를 학습한다 그리고 그 다음 새로운 공변량 조합 xnew에 연관하는 출력 o(xnew)를 예측하기 위해 사용할 수 있다. 함수 compute는 이 계산을 간단하게 한다. 그것은 자동으로 주어진 신경망의 구조를 재정의한다 그리고 임의의 공변량 조합의 출력을 계산한다.
예제를 유지하려면, 예측된 출력은 예로 age=22, parity=1, induced ≤ 1, 그리고 spontaneous ≤1을 가지는 결측치 조합을 계산할 수 있다. 그들은 new.output$net.result에서 주어진다.
> new.output <- compute(nn,
covariate=matrix(c(22,1,0,0,
22,1,1,0,
22,1,0,1,
22,1,1,1),
byrow=TRUE, ncol=4))
> new.output$net.result
[,1]
[1,] 0.1477097
[2,] 0.1929026
[3,] 0.3139651
[4,] 0.8516760
이것은 언급된 공변량 조합으로 주어진 경우의 예측 가능성을 의미한다, i.e. o(x)는, 이 예에서 이전 낙태의 수를 가지고 증가한다.
confidence.interval 함수 (The confidence.interval function)
신경망의 가중치는 다변량 정규 분포를 따른다 만약 망이 식별 가능하다면(White, 1989). 신경망은 구별된다 만약 그것이 입력 층이나 숨김 층에 관계 없는 뉴런을 포함하지 않는다면. 입력 층에서 관계가 없는 뉴런은 예를 들어 영향이 없거나 또는 포함된 다른 공변량의 선형 조합의 공변량일 수 있다. 만약 이 제약이 만족한다면 그리고 에러 함수가 음의 로그-우도와 같다면, 신뢰 구간은 각 가중치에서 계산할 수 있다. neuralnet 패키지는 모든 제약이 만족되는지에 관계 없이 이런 신뢰 구간(confidence intervals)을 계산하는 함수를 제공한다. 그러므로, 사용자는 결과를 해석하는데 주의해야 한다.
그러므로 공변량 age는 결과에 영향을 가지지 않는다 그리고 연계된 뉴런은 그러므로 관계가 없다, 새로운 신경망(nn.new), 단지 3개의 입력 변수 parity, induced, 그리고 spontaneous를 가진다, confidence.interval의 사용을 보여주기 위하여 훈련되어야 한다. 모든 제약이 지금 만족한다고 가정하자, i.e. 3개의 입력 변수이든 2개의 숨김 뉴런이든 관계가 없다. 신뢰 구간(confidence intervals)은 그러면 함수 confidence.interval을 가지고 계산할 수 있다:
> ci <- confidence.interval(nn.new, alpha=0.05)
> ci$lower.ci
[[1]]
[[1]][[1]]
[,1] [,2]
[1,] 1.830803796 -2.680895286
[2,] 1.673863304 -2.839908343
[3,] -8.883004913 -37.232020925
[4,] -48.906348154 -18.748849335
[[1]][[2]]
[,1]
[1,] 1.283391149
[2,] -3.724315385
[3,] -2.650545922
각 가중치에서, ci$lower.ci는 연관된 하위 신뢰 구간의 한계 그리고 ci$upper.ci는 연관된 상위 신뢰 구간의 한계를 제공한다. 첫번째 매트릭은 숨김 뉴런을 이끄는 가중치의 제한을 가진다. 열은 2개의 숨김 뉴런을 언급한다. 다른 3개의 뉴런의 출력 뉴런을 이끄는 제한값이다.
요약 (Summary)
이 논문은 다층 퍼셉트론 그리고 감독 학습 알고리즘의 간략한 소개를 제공한다. 그것은 공변량과 응답 변수 간의 함수적 관계의 모델을 구축할 때 적용할 수 있는 패키지 neuralnet에 소개된다. neuralnet은 다층 퍼셉트론을 회귀 분석의 맥락에서 주어진 데이터 셋을 훈련하는 매우 유연함 함수를 가진다. 그것은 매우 유연한 패키지이므로 대부분의 변수를 쉽게 적용할 수 있다. 예로, 활성화 함수 그리고 에러 함수는 임의로 선택할 수 있고 그리고 R에서 일반적인 함수 정의로 정의할 수 있다.





궁금한게 있습니다. 어떻게 입력변수를 공변량이라고 할 수 있나요?
답글삭제