Random Uniform Forests: an overview part 1

Saïp Ciss∗
September 22, 2014

Abstract(개요)

Random Uniform Forests는 Breiman’s Random Forests (tm) (Breiman, 2001)와 Extremely randomized trees (Geurts et al., 2006)의 변형이다. Random Uniform Forests는 분류, 회귀 그리고 비감독 학습을 위해 설계되었다. 그들은 다양한 비가지치기와 무작위 이진 결정 트리(unpruned and randomized binary decision trees)를 구축하는 앙상블 모델(ensemble model)이다. Random Forests와 달리, 이것들은 각 트리의 성장에 무작위 분할-점(random cut-points)을 사용한다. 극대화 랜덤 트리(Extremely randomized trees)와 달리, 이것들은 부트스트랩과 하위표본(bootstrap and subsampling)을 사용한다, 그러므로 Out-of-bag (OOB) 모델링이 핵심 규칙이다. 두 알고리즘과 달리, 각 노드에서, 교체된 표본(sampling with replacement)으로 특징 추출 작업을 수행한다, 알고리즘의 중요 목적은 낮은 상관관계의 트리를 얻고, 변수 중요도의 심도있는 분석을 허용하고 그리고 순수하게 점증적이다. Random uniform decision trees는 모델의 핵심이다. 우리는 알고리즘의 거의 모든 함수를 구현한 R 패키지(randomUniformForest)를 제공한다, 브라이만의 경계(Breiman’s bounds)를 포함하고 그리고 이 개요에서, 우리는 이론적인 주장과 R 코드를 가지고 완전하게 포괄하는 개요를 보여준다.
Keywords : Random Uniform Forests, Variable importance, statistical learning, machine learning, ensemble learning, classification, regression, R package.

1 Introduction

Random Uniform Forests는 분류나 회귀 같은 작업을 처리하기 위해 그들을 결합하기 보단 많은 기본 학습자를 생성하는 앙상블 모델 군에 포함된다. 이것은 나중을 위해 모든 속성을 유지하는 Breiman’s Random Forests 보다 계산적인 비용이 덜 들게 설계되었다. 이것은 Extremely Randomized Trees (Extra-Trees)의 사상을 따른다 그러나, 여기서, 우리는 OOB (Out-of-bag) 평가가 느슨하게 되는 것을 원하지 않는다.
앙상블 학습의 구현은 널리 퍼져있다, 다른 수단을 사용; 어쨌든 우리는 실세계 문제를 R (R core Team, 2014)에서 사용할 수 있게 충분한 알고리즘을 제공하고 그들의 결정 규칙에서 Random Uniform Forests에 근접한 Random Forests와 Extra-Trees에 집중할 것이다. 기본 학습자는 결정 트리이다, CART (Breiman et al., 1984) 같은, 그러나 Random Uniform Forests에서 그들은 비-가지치기이고 결정론적이 아니다.
Random Uniform Forests에서, 우리는 강한 임의성 그리고 전역 최적화의 어떤 종류를 찾는다. 여기서, 우리는 트리의 평균 분산에서 트리(또는 트리 잔차) 간 낮은 상관관계가 되기를 원한다, 결국은, 증가하지만 그렇게 많지 않음. 우리는 편향에 상관하지 않는다, 트리가 충분히 임의적이라면, 앙상블 모델은 낮은 편향을 가진다고 가정하기 때문. 그렇지 않으면, 알고리즘은 편향을 줄이기 위해 설계된 후처리(post-processing) 함수를 제공한다. 관측에서 forest 분류기의 평균과 Y의 평균 간의 편향은 여기서 다르다는 점에 주목. 결론적으로, 우리는 다음 단계를 사용하여 모델을 구축한다.
  • 분류에서, 우리는 먼저 각 트리에서 n개의 훈련 표본 (the bootstrap) 중 n개의 관측을 교체한다. 회귀에서, 우리는 하위표본(n개 중 m개의 포인트, m < n, 교체 없이 생성)을 이용한다.
  • 각 트리는 균등한 표본으로써 성장한다, 교체를 가짐, 각 노드의 변수의 집합. 이것은 문제의 차원이 d 이면, 선택 ⌈ βd⌉ 변수, β ≥ 1/d, 트리가 성장하는 각 노드에서.
  • 각 분할점(cut-point)은 각 후보 변수의 지지도에서 연속적인 균등 분포 또는 각 후보 변수에서 2개의 임의 포인트 간에 더 계산적인 효율성에 따라 임의로 생성된다. 어쨌든, 우리는 최적의 분할점을 찾기 위해 어떤 지역 최적화를 이용하지 않는다. 각각은 연속적인 균등 분포를 정확하게 따르므로 노드의 점들 사이에 그려지지 않는다.
  • 최적의 임의 노드는 정보 획득(Information Gain)을 최대(분류) 또는 L2(또는 L1) 거리가 최소(회귀)로 하여 선택된다.
위의 4개의 요소 각각은 Random Forests 또는 ExtraTrees와 다르다. 중요한 요지는 변수를 가져오는데(교체를 가짐) 있다, 연속적인 균등 분포를 사용 그리고 최적 기준을 선택. 알고리즘 수준에서, 다른 증명이 사용됨에 주목(e.g. 범주형 변수에서 또는 사용하지 않는 변수를 제거함에). Extra-Trees와 Random Forests 둘 모두에서, 변수를 선택할 때 교체가 없다. Extra-Trees는 임의의 분할점을 사용한다, 현재 노드에서 각 후보자 변수의 최대값과 최소값 사이에서 균등하게 가져옴. Random Forests 처럼, Random Uniform Forests는 분류에서 부트스트랩(bootstrap)을 사용한다, 그러나 회귀에서는, 하위표본이 일반적으로 선호된다, 부트스트랩보다 더 나은 결과를 가짐. 3개 알고리즘 모두 각 노드에서 후보자 간에 최적의 분할점과 변수를 찾기 위해 다른 기준을 사용한다.
다음 절에서, 우리는 random uniform decision trees에서 기본학습자의 이론적인 증명에 초점을 맞춘다.
3절에서, Random Uniform Forests를 상세히 한다.
4절에서, 모델의 어떤 유용한 확장성을 보여준다
5절에서, 실세계 데이터 셋을 가지고 어느정도 완전하게 포괄하고 재생산하는 예제를 제공한다.

2 Random uniform decision trees

Random uniform decision trees는 비-가지치기와 임의의 이진 결정 트리이다. 연속적인 균등 분포를 구축하기 위해 사용되고(모델의 이름이 됨) 그리고, CART와 달리, 최적성을 찾지 않는다. 이것들은, 먼저 Random Uniform Forests의 핵심이 되게 사용해야 하고 그리고 하나의 무작위 균등 결정 트리 성장은 필요하지 않다(CART와 비교해서). 그러나 Random Uniform Forests의 이해는 앞의 메커니즘을 아는 것이 먼저 필요하다. 우리는 독자가 결정 트리가 무엇인지 알고 있다고 가정한다; 그것이 특별한 경우에 어떻게 성장하는지에 관련이 있다. (임의의 균등) 결정 트리의 성장은 기본적으로, 3가지 측면을 알 필요가 있다:
- 성장과 노드(부분: region) 를 수정하는 방법,
- 언제 트리 성장이 멈추는지,
- 결정 규칙을 정의하고 구축하는 방법
정의(Definition). 임의 균등 결정 트리(random uniform decision tree)는 무작위 분할점을 사용하여 구축되는 어떤 노드의 이진 트리이다. 재귀 분할의 각 단계에서, ⌈βd ⌉ 변수, β ≥ 1/d, 교체가 된다. 그러면 각 후보 변수에서, 분할점 α는 각 후보자의 지지도 또는 다음의 2개의 임의의 포인트 간에 연속적인 균등 분포를 사용하여 도출된다. 최적의 임의 노드는 정보 획득 최대(분류에서) 또는 회귀에서 L2 거리(또는 다른 하나)를 최소로하여 도출된다. 재귀 분할은 중지 규칙이 일치하지 않는 한 계속 수행한다. 결정 규칙은 적용은 오직 종료 노드에만 존재한다.

2.1 Regions

Random uniform decision trees는 결정 트리의 다른 형식과 비슷하고 그리고 노드는 항상 2 또는 0개의 자식 노드를 가진다. 우리는 몇 라인에서 알고리즘의 상세를 얻을 수 있 있다. 먼저 region이 무엇인지 정의해야 한다 그리고, 우리는 P라 명명함, 데이터의 일부분이다. Devroye et al. (1996)에 따르면, 이 정의를 제안한다.
정의(Definition): A는 부할 P의 region이다, 만약 어떤 B ∈ P, A ∩ B = ∅ 또는 A ⊆ B 이면.
그러므로, 우리는 Dn = {(Xi, Yi), 1 ≤ i ≤ n}, 관측과 훈련 집합의 응답에 해당, (X, Y)는 ℜd × y-값 임의 쌍.
A는 random uniform decision tree의 최적 region 이다, 만약:

2.2 Stopping rules

일단 A와 AC를, 그것의 보완적인 region, 찾는다, 아래의 어떤 조건을 만족할 때 까지 2개의 region(임의의 변수와 분할점에서 유도 그리고 최적 region 선택)을 찾기 위해 재귀 분할을 반복한다:
  • 관측의 최소 수에 도달한 경우,
  • 하나의 region에서, 모든 관측은 같은 구분(label) 또는 값을 가진 경우,
  • 하나의 region에서, 모든 관측이 동일한 경우,
  • 하나의 region에서, 선택할 특징이 더 이상 없는 경우,
  • IG(j, Dn) (또는, 회귀에서, L2(j, Dn))가 임계점에 도달한 경우(보통 0)

2.3 Optimization criterion

지금, 우리는 정보 획득 함수 IG를 정의할 필요가 있다, 그리고 트리에서 결정 규칙, 회귀에서, 우리는 Y ∈ {0, 1}를 가정. 다음으로 정의:
H는 the Shannon entropy(자연 로그를 사용함에 주목) 인 경우, 그리고
0 log 0 = 0을 가짐, 그래서 H(Y) ≥ 0.
라 놓자, 그러면
그리고
이다.
회귀에서는, 다음을 가짐:

2.4 Decision rule

매회 최적 노드 A를 위한 결정 규칙(decision rule) gp을 정의된 중지 규칙이 만족된다. 분류에서 정의:
회귀는:

2.5 Algorithm

아래의 알고리즘으로 위에서 다룬 다른 작업을 요약할 수 있다:
  1. Dn에서 n 관측을 교체(또는 하위표본, n개 중 m, 회귀의 경우에)를 수행.
    • ⌈ βd ⌉ 변수 교체
    • ⌈ βd ⌉ 변수 각각에서, 각 후보 변수의 지지도 또는 2개의 임의 포인트 간에 연속적인 균등 분포를 사용하는 α을 구함,
  2. ⌈ βd ⌉ 변수에서, 분류에서 IG(j, Dn)를 최대 그리고 회귀에서 L2(j, Dn)를 최소로 하는 짝 (j*, α*)를 선택,
  3. (j*, α*)는 regions A와 AC를 정의하는 짝이다.
  4. 중지 규칙에 일치하면, 분할은 중지되고 결정 규칙 gp를 수립,
  5. 그렇지 않으면, A와 AC를 구하기 위해 단계 1에서 5까지 수행.
random uniform decision tree에서, 분할은 설명한 임의성 때문에 크고 깊은 트리(균등이면, 깊이는 log(n)/log(2))가 되게 한다. 그러므로 비-가지치기를 수행하고, 종료 노드는 트리의 분산이 크게 되는 매우 작은 값을 가지게 되는 경향이 있다. 그러나 편향은 낮게 유지된다 그리고 관심있는 속성은 더 임의적이라도 편향에 영향이 없다는 것이다, 그러므로, random uniform decision tree에서 성과는 예측 오차를 달성하는 것이 아니고 높은 분산을 달성하는 것이다. 그것이 너무 많이 증가하는 것을 피하기 위해, 최적화 기준으로 보낸 훈련 표본의 섭동이 주요 논쟁이다. 두번째는 트리 간에 상관관계가 낮기를 원하기 때문에 지역 최적화(local optimization)를 수행하지 않는다: Breiman의 아이디어를 따라, 단일 트리의 분산은 높고 줄이기 힘드므로, 트리가 독립적이면, 그것을 높게 놓아두고(더 다양성을 도입) 그리고 앙상블이 큰 수의 법칙(Law of Large Numbers)을 사용하여 줄이도록 한다. 실제로는, 존재하지 않으며 종속의 수준을 측정하기 위해 상관관계를 사용할 수 있다.
CART와 비교하여, 하나의 단일 random uniform decision tree는 더 큰 분산을 가질 것이다, 그러나 트리의 평균 분산은 CART의 분산 보다 더 낮게 될 것이다. 다음 단계에서는 평균이 예측 오류에 어떻게 영향을 주는지 알아야 한다.

3 Random Uniform Forests

Random Forests이 수행과 같게, 우리는 Random Uniform Forest를 구축하기 위해 random uniform decision trees의 앙상블을 사용했다. 알고리즘은 간단하다 그러나 높은 임의성으로 트리의 단순 평균을 향상시키는 부분이 알고리즘 수준에 있음을 주목할 수 있다. 다른 관점은 Random Uniform Forests는 Bayesian paradigm을 사용한 것이다: forest 분류기는 고정된 데이터셋에서 거의 모든 변수의 결과이다.

3.1 Algorithm

random uniform decision tree의 구조가 알려졌기 때문에, 알고리즘은 몇 줄이 필요하다(그러나 실제로는 매우 많음):
  1. 각 트리에서, b = 1에서 B까지, random uniform decision tree는 성장하고 그것의 결정 규칙을 수립한다
  2. B 트리에서, 규칙 를 적용한다(3.2 절을 보라).

3.2 Key concepts

더 깊이 가기 전에, Random Forests와 Random Uniform Forests 간에 개념의 차이를 주목해야 한다:
Random Forests에서, 트리는 재귀 적 분할의 각 단계에서 몇몇 지역적에서 최적의 region 이기는 하지만 전역 임의의 region 중에서 최적의 region을 선택함으로써 성장된다. Random Uniform Forest에서는, 최적 region은 다양하고, 겹침이 가능하고, 임의의 region 중에서 선택한다. Extremely Randomized Trees에서는 최적의 region은 비-겹침 임의의 regions 중에서 선택된다. 모든 경우에, 수렴이 발생하는 큰 수의 법칙(Law of Large Numbers) 때문에 보증이 가능하다 그리고 트리는 이론적으로 독립이여야 한다.
왜 빠르고 Random Forests와 비교하여 비슷한 성능(회귀의 경우에 때로는 더 좋음)을 가지는 Extra-Trees를 간단히 사용하지 않았는가? 첫번째 이유는 그것은 OOB 평가가 부족하다, 그러므로 각 트리를 성장하기 위해 모든 훈련 예제가 필요하다. OOB 정보는 단지 교차-검증의 평가와 비교하여 더 많이 중요하다. 두번째 이유는 Extra-Trees에서 더 복잡한 최적화 기준과 연계에 있다(분류와 회귀 모두에서). 우리는 다양성을 보장하기 위해 Random Uniform Forests에서 (매우) 단순한 최적화를 찾는다. 세번째는 문제의 차원은 무작위가 증가함에 따라 문제가 된다는 생각한다 그리고, 특히 회귀의 경우에, 차원은 문제의 하나의 핵심 요소이다.
Random Forests와 중요한 차이는 트리의 평균 분산(average variance of trees)이 작아지는 경우 이후에 일반적으로 더 높게 되는(최소한 회귀에서 발생) 평균 트리 상관계수(average trees correlation)에 있다. 낮은 상관관계를 추구하게 된 동기는 큰 수의 법칙과 Random Forests 그리고 실제에 근사하게 되기를 원하는 Random Uniform Forests의 이론적인 속성에, 직접적으로 나타난다. 다른 말로, Random Uniform Forests는 우리가 여기서 더 최적화하기를 바라는 차원 보다는 관측의 관점에서 심하게 무작위로 사용하는 Breiman의 아이디어의 응용(application)이다.

3.3 Decision rule

결정 규칙을 라 하자, θ는 트리에 도입된 무작위를 나타내는 파라메터인 경우. b-번째 트리에서, 1 ≤ b ≤ B, 를 가진다. 트리의 앙상블에서, 결정 규칙은, , 작성하기가 쉽다. 이진 트리에서:
그리고 회귀에서
가진다.
결정 규칙은 단순하다 그리고 관심있는 속성을 어떻게 찾을지 그리고 앙상블 모델의 좋은 결과를 설명하는 방법을 물을 수 있다. Random (Uniform) Forests에서 트리는 그들의 특징 대부분을 적용하기 위해 약한 의존이 되게 설계되었다. Breiman은 Random Forests의 주요 이론적 특징을 소개했다 그리고 Random Uniform Forests는 단순히 그들을 상속한다.

3.4 Convergence of prediction error

먼저 회귀를 보자, mg를 고려, 올바르게 구분된 포인트와 오분류된 포인트 간에 (빈도의) 차이를 측정하는 여분 함수(margin function). 우리는 다음을 가진다:
Breiman의 표기를 따른다는 것을 기억하자, PE*는 예측 오류. 다음을 정의:
그리고 큰 수의 법칙(the Law of Large Numbers)으로, B → ∞일 때,
(Breiman, 2001, 이론 1.2)
회귀에서, 같은 결과를 얻는다:
그리고 B → ∞일 때,
(Breiman, 2001, 이론 11.1)
  • 그 결과로, Random Uniform Forests는 트리가 독립이라면 과적합이 발생하지 않는다(실제로, 약간 의존). 트리 간에 낮은 상관관계는 (이진) 분류에서 쉽게 도달함에 주목할 수 있다(보통 약 0.1) 그러나 회귀에서는 약간 더 어렵다(보통 약 0.3 또는 더 큼).
  • 두번째 결과는 많은 트리가 성장될 필요가 없다. 모델이 실제 예측 오류를 향하는 수렴은 forest에 트리를 추가함에 따라 빠르게 발생한다.
  • 세번째는 분류에서 먼저 편향이 낮게 될 필요가 있고 회귀에서는 먼저 상관관계를 줄일 필요가 있다.
그러나, 수렴의 주요 응용(application)은 일관성에 대한 추가 작업 없이 예측 오류를 줄이는 방법에 단지 초점을 맞출 수 있는 능력이다. 이후에, 회귀의 첫번째 결과는 최근에 얻어졌고(Scornet et al., 2014) 그리고 아마도 흥미로운 개발로 이끌 것이다.

3.5 The OOB classifier

Out-of-bag (OOB)는 트리 구축에 참여하지 않는 관측이다. 각 트리에서, 부트스트랩 또는 하위-표본 때문에, 어떤 관측은 선택되지 않고 결정 규칙이 인 OOB 분류기를 구축하기 위해 저장된다. OOB 분류기는 훈련 표본에서만 존재한다 그리고 B′ 트리, B′ < B, n개의 관측을 가짐. B′ 트리는 평가해야 하는 각 관측과 같을 필요가 없음에 주의하라. 우리는 관측 x와 Dn를 식을 가진다
그리고 회귀에서
는 트리의 집합인 경우, B에 속함, x를 결코 분류하지 않음.
OOB 분류기는 예측 오류의 평가를 제공하고 그리고 크게 향상된다, 후-처리 처럼, 예측 오류 또는 다른 목적으로 통제하기 위해. 가장 중요한 하나는 과적합을 방지하는 방법이다, Breiman의 경계(bounds)와 결합하는 OOB 분류기를 사용.

3.6 Bounds

상관관계가 감소함에따라, 트리의 평균 분산은 증가한다 그리고 그것은 예측 오류를 줄이기 힘들어지기 시작한다. 만약 상관관계와 분산 둘 모두 통제하기를 원한다면, 하나의 방법은 Breiman의 경계(bounds)를 관측하고 주시해야 한다. 예측 오류(i.i.d. 가정하에)는 한계를 넘어 증가하지 않는 것을 보장하는 Random (Uniform) Forests의 경계가 있다. Breiman’s bounds의 대부분은 응용(applications)은 모델을 향상하기 위해 더 많은 작업(또한 n에 의존, 그러나 엔지니어링 특징이 아님)이 필요하거나 알고리즘을 위한 공간이 더이상 없으면 OOB 분류기(경계(bounds)에서 상속)를 통해 연결되고 보여준다. 먼저, 경계는 분류를 포함하고 2개를 가진다. 첫번째 경계는 Bienaymé-Tchebychev 방정식으로,
다음의 경우
mg와 s의 한계이다, s > 0, 강도( 또는 마진)은
첫번째 경계는 예측 오류가 명확하지만 알려지지 않는 한계 아래에 항상 있어야 됨을 나타낸다(OOB 정보를 사용하여 그것을 평가하지 않는다면). 그것은 예측 오류의 상한 경계이다 그러나 느슨하게 할 수 있다(그러나 균형적이지 않은 구분(classes) 또는 더 어려운 문제의 경우에 사용).
두번째 경계는 더 엄격하다. 식(Breiman, 2001, theorem 2.3)을 가짐
다음의 경우
ρ( θ, θ′)은 변수 θ와 θ′인 2개의 트리에서 상관관계 그리고 Var(θ)는 트리의 분산인 경우, 원시 강도의 분산(raw strength)을 나타냄. 이후의 rmg에 주목. 식
그리고
임에 주목할 수 있다.
여기서는 상관관계(감소를 쉽게)와 연계된다 그리고 강도를 더 크게, 편향과 연계. Random Uniform Forests에서, 우리는 더 많은 트리를 추가함으로써 강도가 증가되기를 기대한다. 만약 더 최적화를 시도하면, 강도는 증가하지만 또한 상관관계 역시 너무 증가할 것이다. 운좋게도, 강도에 너무 많은 영향이 없이 (한도까지) 더 심한 무작위로 상관관계를 낮출 수 있다. Breiman’s second bound를 예측 오류의 기대 경계(expected bound of prediction error)라 부른다 그리고 우리가 찾는 하나의 결과는 초과되지 않아야 한다, OOB에러를 생각하라. 경계는 불균형 구분(class) 또는 상관 공변량(correlated covariates)의 경우에 작동하지 않을 수 있음에 주의한다.
회귀에서, Breiman은 forest의 경계와 이론적인 예측 오류를 제안했다. 분류와의 중요한 차이는 아래의 사실에 있다:
  1. 경계는 보통 상한 경계가 없다 왜냐하면 회귀에서 상관관계는 분류에서 보다 훨씬 더 크다 그리고 아마도 수렴을 방해한다.
  2. 예측 오류가 어디에 밀어 넣을 수 있는지를 명시적으로 알려준다.
  3. 트리의 (평균) 공변량과 더 강하게 연계된다.
모든 θ에서, E(Y) = EX(gp(X, θ))를 가정하자. 식 (Breiman, 2001, theorem 11.2)
다음의 경우에
는 트리 잔차 간에 평균 상관관계(average correlation between trees residuals)이다.
게다가, 우리는 다음으로 주어진 forest의 이론적인 예측 오류 추정자(estimator of the theoretical prediction error of the forest)를 가진다:
회귀에서 상관관계와 트리의 평균 예측 오류 둘 모두에 관계한다(그리고, 그다음, 트리의 분산). 여기서, 매번 낮은 분산을 원하고, 상관관계는 두개가 약화되는 방법을 찾지 못한다면 증가한다. 무작위는, 아직까지, 상관관계를 줄이는 열쇠이다. 분산이 높아지는 것을 피하기 위해, 하나의 전략은 차원(dimension)에서 더 많이 작업해야 한다, 트리를 크고 깊게 성장(또한 편향의 감소시키기 위해 이용) 그리고, 많은 경우에, 후-처리 작업해야 더 한다. 회귀에서, 중요 문제는 무작위는 분산에 영향을 주는 많은 조합을 해야 하지만 그러나 상관관계는 충분히 줄어들지 않는다는 점이다. 결과적으로, 많는 실험에서, 분산의 감소 없이 상관관계는 0.3 또는 0.4를 넘을 수 있다.
2가지 점에 주의:
  • 충분히 낮지 않은 상관관계 때문에, 문제의 일부는 충분한 다양성이 생기지 않도록 부트스트랩을 연계한다. 이것이 회귀에서 Random Uniform Forests를 사용하지 않는 이유이다.
  • 높게 남아있을 수 있는 분산 때문에, 경쟁을 증가시키기 위해 교체로 각 노드에서 변수를 가져오게 허용해야 한다, 그래서 상관관계의 낮은 비용(되도록 낮게)에서 트리의 평균 분산을 줄이려고 시도해야 한다.
기쁜 소식은 Random (Uniform) Forests에서 예측 오류를 줄이기 위해 충분한 여지가 있는 것처럼 보인다는 것이다. 그것에 접근하는 하나의 방법은 OOB 분류기를 사용하여 forest의 이론적인 예측 오류를 감시해야 한다. 그렇지 않다면 과적합 가능성에 주의해야 한다.

3.7 Decomposition of prediction error and OOB bounds

Y와 X의 관계가 알지 못한다고 여기서 가정한다. 오로지 1차와 2차 정렬의 중요성만 기대한다(그리고 i.i.d. 가정) 그러면, 나중에 제어를 위해 확인하기 위한 위치를 찾기 위해 예측 오류를 분해할 수 있다. 식, 이진 분류(Y ∈ {0, 1}),
그리고 회귀에서,
Breiman의 경계를 OOB 범위로 대체하면 OOB 경계가 주어지고, OOB 경계는 테스트 오류의 상한선이 된다 (알고리즘과 예측 오류를 완전히 제어할 수 있게 한다). 약간의 조건과 i.i.d. 조건 하에 (Ciss, 2015c), 다음을 얻을 수 있다:
는 OOB 경험적 오류(훈련 집합에서 계산됨)이고 는 검증 에러인 경우.
프레젠테이션의 첫 번째 부분을 완성하기 위해, 후-처리, 특징의 임의 조합 또는 외삽(extrapolation)과 같은 몇 가지 추가 단계를 생략하고 그리고 해석에 중점을 두어 모델링에 중요한 열쇠를 제공한다.

3.8 Variable importance

Random Forests에서 처럼, 변수 중요도의 측정을 제공한다. 사실, Random Uniform Forests는 변수 중요도의 평가를 더 깊이 얻을 수 있게 만들었다.
첫번째 특징은 global variable importance이다, 최적화 기준을 사용하여 직접 계산됨. VI가 중요도 점수이면, j-번째 변수에서, 1 ≤ j ≤ d; 최적이면 j*라 명명함,
그리고, 회귀에서
Kb는 b-번째 트리에서 region의 수 이다, 1 ≤ b ≤ B. 그러면, 계산으로 상대 영향을 측정한다. 하나의 변수가 결코 최적이 안된다면(기준에서), 그러면 결코 측정되지 않고 그리고 그것의 영향도는 널(null)이 된다. 전역 변수 중요성이 어떤 변수가 유입되는지를 알려주지 만, 하나의 중요한 변수가 응답에 어떻게 영향을 미치는지에 대해서는 여전히 알지 못한다. 이에 접근하기 위해 지역 변수 중요성 개념에서 부분 종속성에 이르기까지 다양한 측정을 제공한다. 이것은 헌신적인 논문 Variable importance in Random Uniform Forests(Ciss, 2015b)에서 세부 정보를 찾을 수 있을 것이다.

4 Some extensions

이 절에서는, Random Uniform Forests의 약간의 다른 개발을 빠르게 소개한다. 예측과 신뢰 구간(prediction and confidence intervals )으로 시작해서, 그다음 출력 섭동 표본(output perturbation sampling)에대해 간략하게 말한다, Random Forests의 약간의 숨겨진 가치를 얻게 한다, 그리고 점증적 학습(incremental learning)으로 끝낸다.

4.1 Prediction and confidence intervals

실제 삶의 문제로 갔을 때 또는 산업 사례가 표준 사례가 될 때, 주요 문제는 평균적인 예측 정밀도를 제공하지는 않지만, 그러나 알려진 것이 발생할 것이라는 강력한 보장을 제공한다. 첫번째 옵션은 교차-검증 또는 OOB classifier와 errors를 사용한다. 회귀에서, 통상은 예측 값을 원하는 것이 아니라, 정확하게 일치하기 어려움, 그러나 예측 구간을 가지는 예측 값 그리고, 변수에서, 예측 구간을 원하는 것이다. 더 분명하게 만약, 예로, 문제가 어떤 금전적인 위험이나 비용이 포함한다면, 단지 예측 값에 의존함은 위험할 것이다. 더 흥미로운 점은, 대신에, 버튼을 누르는 사람에게 약간의 다른 정보를 준다는 것이다.
Random Uniform Forests는 어떤 예측과 신뢰 구간을 만들기 위한 특히 실제 생활을 위해 특별히 설계된 새로운 접근을 제공한다. 그런 경우의 동기에 대해 논의하지 않는다, 그러나 그런 구간을 생성하기 위한 절차를 바로 제공한다.
라 표기하자, α는 i-번째 관측에서 gp 분포의 경험적인 분위수를 요구한다. 보통 다음의 관계를 가진다: 확률 1 - α, 그리고 전체에서 i ∈ [1, n], 모든 Yi에서 부트스트랩 신뢰 구간의 식:
이후의 작업은 좋다 그러나 보통은 너무 크고 그리고 때로는 실제에 사용하기 어렵다.
대안으로, 각 Yi에서, 우리는 다음의 대안을 고려한다,
  • 교체를 통해 G(Xi, B) = { gp(1)(Xi), gp(2)(Xi), …, gp(B)(Xi)}의 Si 추정을 유도한다, S는 G(Xi, B)의 유일 값의 수인 경우. 그러면, Yi의 첫번째 추정자를 다음으로 계산할 수 있다:
    gp(s)(Xi)는 임의로 선택되는 경우.
  • 연산 K 회를 반복으로 K-표본 을 유도한다.
  • 그러면 을 고려한다. α는 K-표본의 분포의 경험적인 분위수 순서이다. 이것은 Yi에서 직접 사용할 수 없다, 예측 구간을 고려할 때 지수적인 하나, 작거나 매우 많은 빈도(그리고 근접)한 분포는 주로 어려운 문제이기 때문. 가정은, 분위수의 이웃에서, 경험적 분포는 가우시안이다 그러면, 아래의 예측 구간을 정의한다: 근접 확률(approached probability) 1- α를 가짐,
    Zα/2는 N(0, 1) 가우시안 분포의 α/2 순서 분위수인 경우,
    은 값이 Xi에서 유일한 값에서 결정 규칙의 경험적 분산이다.
    그러면, 예 Y‾로 말하는 변수의 신뢰 구간이 유도된다.
    다음을 가짐:
    그러면, 근접 확률(approached probability) 1 - α를 가짐,
  • 마지막 단계는 OOB 정보를 사용하거나 또는 유효한 표본을 가지고 검증한다.

4.2 Output perturbation sampling

출력 섭동 표본(Output perturbation sampling)은 Random Uniform Forests의 가장 이상하다 그래서 이것을 먼저 설명한다. 알고리즘이 오직 회귀인 경우만 고려하자: 각 트리에서, Dn의 관측 n개 중 m개의 하위표본과 성장 과정. 출력 섭동 표본은 아래의 과정을 나타낸다: 각 트리에서, Dn의 관측 n개 중 m개의 하위표본, 전체(혹은 일부) Yi 값의 교체, 1 ≤ i ≤ m, 변수 Z에서 유도되는 임의의 값, 인 경우, c ≥ 1, 그러면, 트리를 성장.
출력 섭동 표본은 사용했을 때, 어떤 결과는 경험적으로 관측된다:
  • 과적합은 거의 발생하지 않음
  • 상관관계는 (팩터 3까지) 급격하게 감소, 그렇지만 분산 역시 증가,
  • 예측 오류는 약간 증가한다, 어떤 경우에는 더 좋음.
세번째 특징이 많은 경우에서 발견되므로 가장 놀랍다, 전부는 아니지만, 예측 오류는, 사실, 어떤 (자동) 후-처리 후에 표준인 경우와 비슷하다. 이것은 모델이 단지 매개 변수 (parameters)만 필요하게 보인다. 다른 말로, 단지 비-상관 트리가 많은 성장하더라도, 수렴이 발생하고, 예측 오류는 Y 분포의 매개 변수(parameters)의 추정치만 알고 있는 한 낮게 유지된다.

4.3 Incremental learning

점증적 학습(Incremental learning)은 연속적인 데이터(streaming data)에서 학습 방법이다. 데이터가 매우 크거나 정크(chunks)로 입력되는 경우이면, 점증적 학습은 그들의 크기에 관계없이 처리하는 하나의 방법이다. 그러나, 적어도 정밀도의 손실에서 일반적으로 많은 비용이 든다. 점증적 학습이 데이터의 정크에서 진행하고 그리고 회귀의 경우는 낮은 예측 오류를 달성하기 위해 분류보다 더 쉽지 않다(한번에 전체 데이터를 계산하는 것과 대조적).
점증적 학습은 2가지 경우를 가진다:
  • i.i.d. 가정은 모든 정크에 적용된다(혹은 많은 정크),
  • (X, Y)의 (결합(joint)) 분포는 변화한다(분포 자체나 또는 그것의 매개변수).
Random Uniform Forests는 기본적으로 점증적이다, 분포의 변화에서 조차, 그러나 약간의 작업이 요구된다. 출력 섭동 표본(Output perturbation sampling)은 불규칙한 예측 오류를 보지 못하는 복잡한 것들의 일부이다. 분류의 경우는 더 단순하다, 분류에서 수행하기 위한 방법을 알고리즘 자체를 변경하도록 할 수 있다, i.e., 중요 선택(majority vote)의 결과를 결정하는 임계점을 변경할 수 있다.
변화하는 분포의 일반적인 경우를 고려하자: 결정 규칙은 모든 경우에서와 같다, 그러나 forest 분류기를 적용하기 위해 OOB 분류기(그리고 다른 도구)에 의존해야 한다. 점증적인 forest 분류기를 라 하자, 우리는 단순하게 다음을 얻는다:
회귀에서
은 시간 구간 t에서 데이터의 일부이고, Bt는, 시간 구간 t에서 트리의 수이고, T는, 시간 구간의 수인 경우.
점증적 학습은 데이터와 결정 규칙 모두를 적용하는 하위표본 생성 과정(subsampling process)이다. 각 트리는 오로지 데이터의 일부만 보여준다 그리고 forest 그 자신은 데이터의 (더 큰) 부분을 본다. 여기서 주요 논쟁은 분할점이 무작위이다, 그래서, 많은 것들이 변화하지 않는 부분 또는 전체 데이터를 본다. 그리고 문제가 발생하더라도, 다른 옵션이 없다. 문제는 획득된 정보에 더 많이 의존한다. 시간 구간에서 중요한 어떤 정보는, 다음 시간 구간에서 절대적이거나 나빠질 수 있다, forest에 혼동을 유발. 오로지 희망은, 그러면, 앞서 기억된 모든 정보의 손실 없이 새로운 상황에 분류기를 적용시킨다. 하위- forest도 forest이기 때문에, 트리의 약간의 손실(OOB 분규기 같은)로 , , 평가로 Random Uniform Forests 를 적합할 수 있다. 트리를 결코 수정하지 않음에 주목할 수 있다: 그러나 재호출되고, 복제되고, 제거되거나 저장되고, 혹은 추가된다.



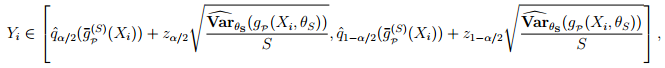
댓글 없음:

댓글 쓰기

피드 구독하기: 댓글 (Atom)