Stephen Milborrow
September 10, 2016
September 10, 2016
출처: Stephen Milborrow Homepage
원본: PDF
Contents
- 1 Introduction
- 2 Overview
- 3 Termination conditions for the forward pass
- 4 Generalized linear models
- 5 Factors
- 6 The linpreds argument
- 7 The allowed argument
- 8 Using earth with fda and mda
- 9 Plots
- 10 Cross-validating earth models
- 11 Understanding cross-validation
- 12 Estimating variable importance
- 13 FAQ
4 일반화 선형 모델(Generalized linear models)
만약 glm 인수를 명시하면 Earth 는 일반화 선형 모델(Generalized Linear Model: GLM)을 생성한다. Earth는 일반적인 모델을 생성하고 그런 다음 MARS 기저 메트릭 bx 에서 glm 을 호출한다.
더 상세하게, 모델은 다음처럼 생성된다. Earth는 먼저 표준 MARS 모델을 생성한다, 가지치기 패스 후에 bx에서 m.fit을 호출을 내부적으로 내포함. (Figure 1과 섹션 2.5 "가지치지 패스(The pruning pass)"를 보라) 그러므로 knot 위치와 조건(terms)는 여느 때와 같이 결정이 되고 그리고 earth의 리턴 값에서 모든 표준 필드가 나타날 것이다. Earth는 그러면 earth에 전달한 glm 인수에서 명시된 파라메터를 가지는 bx에서 응답을 위해 glm을 호출한다. 다중 응답 모델에서(y가 다중 컬럼을 가질 때), glm 호출은 각 응답에 대해 독립적으로 반복된다. 결과는 earth의 리턴 값에 3 개의 여분의 필드로 보낸다: glm.list, glm.coefficients, 그리고 glm.bpairs.
Earth가 glm를 내부적으로 호출하는 것은 glm 인수 x, y 그리고 model을 TRUE 설정하여 생성된다(이러한 인수를 대한 더 많은 정보를 위해 glm 문서를 보라).
모델을 보기 위해 일반적인 summary(earth.model)를 이용해라. 더 상세하고 보기 위해 summary(earth.model, details=T)를 사용해라, 그러나 프린트된 GLM 상관계수 p 값은 의미가 없음을 기억하라(FAQ 13.8).
glm 모델을 그리기 위한 plot.glm을 호출하기 위해 plot(earth.model$glm.list[[1]])을 사용해라.
earth에서 GLM을 위해 사용된 접근은 Jane Elith 와 John Leathwick에 의해 수행한 작업에서 동기가 되었다([15]는 대표 논문이다)
4.1 GLM 예제(GLM examples)
아래의 예제는 earth-glm모델을 어떻게 명시하는지 보여준다. 예제는 문법만 예시하였다 그리고 필요한 유용한 모델은 아니다. 예제의 어떤 것은, pmethod="none", 이렇게 하지 않으면 이런 인위적인 모델을 가지면 earth는 조건(term) 인터셉트를 제외한 모든것을 가지치는 경향이 있다. 당신을 일반적으로 pmethod="none" 사용을 원하지 않을 것이다. 또한, trace=1, 그러면 이러한 예제를 실행한다면 당신은 earth가 입력 메트릭스를 어떻게 확장하는지 볼 수 있다(Chapter 5 "Factors" 와 Section 4.2 "Binomial pairs"에 설명과 같음).
(i) 두개의 수준 펙터 또는 논리 응답(Two-level factor or logical response). 이 응답은 1과 0을 가지는 하나의 컬럼으로 내부적으로 변환된다.
a1 <- earth(survived~., data=etitanic, trace=1, glm=list(family=binomial))
# equivalent but using earth.default
a1a <- earth(x=etitanic[,-2], y=etitanic[,2],
trace=1, glm=list(family=binomial))
함수 plotd는 이러한 응답에서 유용할 수 있다는 것을 다룬다(Section 9.4).
(ii) 펙터 응답(Factor response). 이 예제는 두 수준 보다 더 많이 가지는 펙터를 위한 것이다.(단지 2 수준을 가지는 펙터는, 이전 예제를 보라.)
a2 <- earth(pclass~., data=etitanic, trace=1, glm=list(family=binomial))
펙터 pclass는 3개의 지시자 컬럼으로 확장된다. (pclass가 이진으로 처리되는 경우인 직접 glm을 호출한다면 이것이 무엇이 다르게 발생하는지 주목해라: 첫번째 수준 대 다른 모든 수준). "masking problem" 때문에, 우리는 2 수준 보다 더 많이 응답하는 펙터에 FDA를 고려하여 다뤄진다.
(iii) 짝 컬럼을 가지고 지정된 이항 모델(Binomial model specified with a column pair). 이것은 하나의 응답 모델이지만 그러나 컬럼의 짝을 가지고 지정한다(Section 4.2 "Binomial pairs) . 다양하게, 이 예제는 probit link를 사용하고 그리고 불필요하게 maxit을 증가시킨다.
ldose <- rep(0:5, 2) - 2 # V&R 4th ed. p. 191
sex <- factor(rep(c("male", "female"), times=c(6,6)))
numdead <- c(1,4,9,13,18,20,0,2,6,10,12,16)
pair <- cbind(numdead, numalive=20 - numdead)
a3 <- earth(pair ~ sex + ldose, trace=1, pmethod="none",
glm=list(family=binomial(link=probit), maxit=100))
(iv) 2배의 이항 응답(Double binomial response)은 (i.e., 다중 응답 모델) 2개의 짝 컬럼을 가지고 지정한다.
numdead2 <- c(2,8,11,12,20,23,0,4,6,16,12,14) # bogus data
doublepair <- cbind(numdead, numalive=20-numdead,
numdead2=numdead2, numalive2=30-numdead2)
a4 <- earth(doublepair ~ sex + ldose, trace=1, pmethod="none",
glm=list(family="binomial"))
(v) 포아송 모델(Poisson model).
counts <- c(18,17,15,20,10,20,25,13,12) # Dobson 1990 p. 93
outcome <- gl(3,1,9)
treatment <- gl(3,3)
a5 <- earth(counts ~ outcome + treatment, trace=1, pmethod="none",
glm=list(family=poisson))
(vi) 표준 earth 모델(Standard earth model), 먼 길. identity link를 가지고 family=gaussian을 사용하는 표준 earth 모델과 똑같은 glm 모델을 생성한다.
a6 <- earth(numdead ~ sex + ldose, trace=1, pmethod="none",
glm=list(family=gaussian(link=identity)))
print(a6$coefficients == a6$glm.coefficients) # all TRUE
4.2 이항 짝(Binomial pairs)
이 절은 만약 당신이 이항 또는 준이항( binomial or quasibinomial family.)을 가지는 earth의 glm 인수 사용한하면 오로지 관계가 있다
glm 함수의 사용자는 성공 수를 위한 컬럼과 실패 수를 위한 컬럼을 가지는 2-컬럼 메트릭의 이항 응답을 지정하는 기술에 친숙할 것이다. 인수 glm=list(family=binomial)이 주어질 때, earth는 그런 컬럼에 y에 표현되었을 때 자동으로 탐색한다(2개의 컬럼 모두 1보다 큰 요소를 가지는 인접한 컬럼을 찾는 것으로). 첫번째 컬럼을 단지 표준 earth 모델을 생성하기 위해 사용된다. 둘 모두 그 다음 earth 가 내부적으로 glm을 호출하여 전달된다.
당신은 bpairs 파라메터를 포함하는 것으로 자동 탐색을 덮어 쓸 수 있다. 이것은 일반적으로 (항상?) 불필요하다. 예를 들어
glm=list(family=binomial, bpairs=c(TRUE, FALSE))
위 문장은 첫번째와 짝을 이루는 두번째를 가지는 응답에서 2-컬럼이다. 이러한 예제는
glm=list(family=binomial, bpairs=c(TRUE, FALSE, TRUE, FALSE)) glm=list(family=binomial, bpairs=c(1,3)) # equivalent
1번째와 2번째 컬럼은 이항 쌍이고 그리고 3번째와 4번째 컬럼은 다른 이항 쌍을 지정한다.
5 펙터(Factors)
이 장은 데이터에서 펙터는 메트릭스가 MARS 엔진에 전달되기 전에 어떻게 "확장(expanded)" 되는지 설명한다.
펙터가 확장된 후에 x와 y의 컬럼 이름을 보기 위해서는 trace=1 또는 높게 사용해라.
5.1 예측자에서 펙터(Factors in the predictors)
Earth는 표준 R 모델에서 lm같은 방식으로 식의 오른쪽에 있는 펙터를 처리한다. 그러므로 펙터는 contrasts의 현재 설정을 사용하여 확장된다. 이것은 earth가 식 또는 x, y 인터페이서를 통해 호출 할 지 아닌지를 결정한다.
5.2 응답에서의 펙터(Factors in the response)
Earth는 비-표준 방식인 다중 응답을 다루는 earth의 능력을 사용하여 응답의 펙터를 처리한다. 이것은 식 또는 x, y 인터페이서를 통해 호출 할 지 아닌지를 결정한다.
2 수준 펙터(또는 논리값)는 1 또는 0의 하나의 지시 컬럼으로 변환된다.
3개 또는 더 많은 수준의 펙터는 1 또는 0의 k 지시 컬럼으로 변환된다, k는 수준의 수이다. (다른 말로, contrasts 메트릭은 항등 행렬(identity matrix)이다, contr.earth.response의 도움말 페이지를 참조하라) 이것은 options("contrasts") 설정에 관계 없이 발생한다 그리고 펙터가 정열인지 또는 비-정열인지 관계가 없이 발생한다. 예를 들어, y의 컬럼이 수준 A, B 그리고 C 이면, 컬럼은 아래와 같이 3개의 컬럼으로 확장된다(실제 데이터는 다양하지만 각 행(row)은 1개 값을 가질 것이다):
(구분에서, 식의 오른쪽에 있는 표준 대조 처리(standard treatment contrast)는 x 메트릭에서 선형 의존을 방지하기 위해 첫번째 "A" 컬럼에 값이 없다. 상세를 위해 contrasts의 도움말 페이지를 보라.)
| A | B | C | #각 펙터 수준의 하나의 컬럼 |
| 0 | 1 | 0 | #각 행(row)은 1개의 1값을 가진다 |
| 1 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 0 | 1 | |
| .... | |||
다중 컬럼에서 이 확장(2 수준 보다 더 많이 가지는 펙터에서 오로지 발생함)은 earth 2.9 절 "Multiple responses"에 설명된 다중 응답 모델을 생성한다는 의미이다.
y에서 짝 이항 응답(paired binomial response) 컬럼은 별도로 처리된다(4.2 절 "Binomial pairs").
5.3 펙터 예제(Factor example)
여기에 승객 등급을 예측하기 위한 etitanic 데이터를 사용하는 예가 있다(반드시 해야 할 의미있는 것은 아님):
> data(etitanic) > head(etitanic) # pclass and sex are factors pclass survived sex age sibsp parch 1 1st 1 female 29.000 0 0 2 1st 1 male 0.917 1 2 3 1st 0 female 2.000 1 2 > earth(pclass ~ ., data=etitanic, trace=1) # note col names in x and y below x[1046,5] with colnames survived sexmale age sibsp parch y[1046,3] with colnames 1st 2nd 3rd rest not shown here...
6 linpreds 인수(The linpreds argument)
linpreds 인수를 가지고, 우리는 어떤 예측자들이 선형(linearly)으로 입력될 것이지 구별할 수 있다, hinge 함수를 사용하는 대신에.
우리는 이것을 유용하게 사용될 수 있는 단순한 예를 준다. 표준 earth 모델로 시작.
fit1 <- earth(Volume ~ ., data = trees) plotmo(fit1)
우리는 Height(높이)가 Girth(둘레) 만큼 중요하지 않다는 점을 plotmo 그래프에서 또는 evimp를 실행하여 확인한다. Girth 는 Volume(부피)의 지표보다 더 신뢰성이 있다고 상호 비교하는 시각 증거를 위해(For collaborative visual evidence), pairs 플롯의 마지막 행(row)을 보라(보기 없음);
pairs(trees, panel = panel.smooth)
우리는 데이터를 설명하는 가장 단순한 모델을 원하기에, 우리는 Height가 선형(linearly)으로 입력될 것이라 결정할 것이다, hinge 함수에서 아님(Figure 2, bottom row);
fit2 <- earth(Volume ~ ., data = trees, linpreds = "Height") summary(fit2)
산출
coefficients
(Intercept) 4.221
Height 0.343 # Height enters linearly
h(14.2-Girth) -3.199
h(Girth-14.2) 6.405
이 예에서, 두번째로 단순한 모델은 첫번째 모델과 거의 같은 R2를 가진다.
6.1 linpreds 지정(Specifying linpreds)
우리는 모든 예측자들이 이처럼 선형으로 입력되게 만들 수 있다(하나의 TRUE 는 linpreds의 길이 만큼 재사용된다) :
earth(Volume~., data=trees, linpreds=TRUE)
linpreds를 지정하는 다른 방법들:
earth(Volume~., data=trees, linpreds=2) # column index in x
earth(Volume~., data=trees, linpreds=c("Height","Girth")) # multiple variables
grep는 linpreds 가 character vector일 때 매칭하기 위해 사용된다. 그러므로 "wind"는 그들의 이름에서 "wind"를 가지는 모든 변수들을 매칭할 것이다. 정규 표현식(regular expression) 변수 이름이 "wind"만 일치하기 위해 "^wind$"를 사용해라
지금 구현에서, 선형으로 입력된 예측자를 위한 GCV 패널티는 knots를 가지는 예측자와 같다. 하나는 상당히 정확하지 않다는 주장을 할 수 있다; 선형 조건(linear term) 덜 불이익을 받는다. (이것은 우리가 a priori가 선형 변수를 처리하기 위한 결정을 만들거나 또는 같은 데이터에서 예비 모델(preliminary model) 생성에 기반한 결정을 만드가에 따라 의존한다.)
 |
| Figure 2: linpreds 인수
상단 행(row): 나무 데이터의 표준 earth 모델 하단 행(row): 같음, 그러나 Height를 가지고 선형으로 입력(linpreds="Height") |
6.2 lm과 같은 모델 생성(Generating the same model as lm)
때로 우리는 lm과 같은 모델 생성하기를 좋아할 것이다, 모든 예측자가 선형 입력인 경우. 그러나 linpreds 인수는 예측자는 모델에 입력되야 한다고 규정하지 않는다, 단지 그것을 입력하면 그것은 선형으로 입력될 것이다: 만약 변수가 추가적인 예측 강도가 미미하다면, earth는 그것을 포함하지 않는다. earth 가 모든 변수를 포함하는 우도(likelihood )를 증가시키기 위해, 아래의 인수 둘 모수 사용해라.
| (i) | thresh=0. 순방향 패스(forward pass)에 만약 그것이 매우 작은 예측 강도를 가지더라도 예측자를 포함하라고 말한다(3장, 마지막 파라그래프). 선형 의존 변수는 여전히 배제될 것임을 주목하라. |
| (ii) | penalty=-1. 역방향 패스(backward pass) 어떤 조건을 버리지 말라고 말한다(FAQ 13.15). 또한 전방향 패스(forward pass)가 GRSq 너무 음수이기 때문에 종료되는 것을 방지한다(3장 condition (iv)). |
예:
earth(Volume~., data=trees, linpreds=TRUE, thresh=0, penalty=-1)
7 허용 인수(The allowed argument)
변수가 허용된 인수로 MARS 조건 입력을 허용하는 방법을 지정할 수 있다. 순방향 패스(forward pass)의 각 단계에서, earth는 변수에서 최적의 해결책(knot)를 찾은 후에 allowed 함수를 호출한다. 잠재적인 조건(term)은 허용 함수가 TRUE를 반환하는 경우에만 포함시킬 것으로 간주한다. 기본 함수는 항상 TRUE를 리턴한다.
당신의 allowed 함수는 다음과 같은 프로토타입(prototype)을 가질 것이다.
function(degree, pred, parents, namesx, first)
에서
| degree | 후보 조건의 상호작용 도수. 추가 조건을 위해 1이 되게 하라. |
| pred | 후보 예측자의 인덱스이다. pred에서 예측자의 인텍스는 펙터가 확장된 후에 입력 메트릭스 x 에서 열의 순서이다. 확장된 후에 컬럼 이름을 보기 위해 earth의 trace=1 인수를 사용해라 |
| parents | dirs에서 후보자 부모 조건의 행(row) 이다 |
| namesx | 옵션 그리고 펙터가 확장된 후에 x의 열(present) 이름이다. |
| first | 옵션 그리고 만약 부모가 TRUE이면 첫번채 allowed 함수는 현재 모델에서 호출된다, 그리고 다음에는 FALSE, i.e. earth의 호출마다 한번 TRUE이다. |
7.1 예(Examples)
인터페이스는 유연하지만 약간의 프로그래밍이 요구된다. 우리는 단순한 예제로 시작한다, 모델에서 하나의 예측자를 완전하게 배제하는 경우.
example1 <- function(degree, pred, parents) # returns TRUE if allowed
{
pred != 2 # disallow predictor 2, which is "Height"
}
a1 <- earth(Volume ~ ., data = trees, allowed = example1)
print(summary(a1))
그러나 이것은 많이 사용되지 않는다, 왜냐하면 earth를 호출할 때 입력 메트릭스에서 예측자를 배제하는 것이 단순하기 때문이다.
a1a <- earth(Volume ~ . - Height, data = trees)
아래의 예는 더 유용하다. 이것은 지정된 예측자가 상호작용 조건에서 사용되는 것을 방지한다. (예는 인위적이다 왜냐하는 이것은 오존 데이터에서 상호작용으로 유일한 출력이 습도(humidity)만 이기를 바라지 않는다.)
example2 <- function(degree, pred, parents)
{
# disallow humidity in terms of degree > 1
# 3 is the "humidity" column in the input matrix
if (degree > 1 && (pred == 3 || parents[3]))
return(FALSE)
TRUE
}
a2 <- earth(O3 ~ ., data = ozone1, degree = 2, allowed = example2)
print(summary(a2))
위 코드의 상세: parents 인수는 dirs 메트릭에서 후보 부모의 행(row)이다(dirs은 earth 도움말 페이지의 Value 절에 설명되어 있다.) parents의 각 요소는 0, 1, -1, 또는 2 그리고 예측자 인텍스에서 parents를 가리킨다. 그러므로 만약 pred가 부보 조건에 있으면 parents[pred]는 0이 아니다. (그렇다, 이것은 혼란스럽다. 아마도 가장 쉬운 접근은 이 장에서 당신이 원하는 예제를 찾는 것이다, 그리고 필요에따라 그것을 수정한다.)
아래의 예는 상호작용 조건에서 지정된 예측자만 허용한다. 상호작용은 allowed.set에 있는 예측자만 허락한다, 필요에 맞게 변경할 수 있음.
example3 <- function(degree, pred, parents)
{
# allow only humidity and temp in terms of degree > 1
# 3 and 4 are the "humidity" and "temp" columns
allowed.set = c(3,4)
if (degree > 1 && (all(allowed.set != pred) || any(parents[-allowed.set])))
return(FALSE)
TRUE
}
a3 <- earth(O3 ~ ., data = ozone1, degree = 2, allowed = example3)
print(summary(a3))
7.2 허용된 함수에서 인덱스 대신에 예측자의 이름 사용
(Using predictor names instead of indices in the allowed function.)
옵션 namesx 인수를 사용하여 인덱스 대신에 예측자의 이름을 사용할 수 있다. 표현된다면, namesx는 펙터가 확장된 후에 x 의 열 이름이다. 위에서 첫번째 예(Height를 허락하지 않는 하나)는 다음과 같이 쓸 수 있다:
example1a <- function(degree, pred, parents, namesx)
{
namesx[pred] != "Height"
}
다음 페이지는 몇 개의 예제를 더 가진다
#--- no predictor in PREDICTORS is allowed to interact with any predictor in PARENTS
#--- but all other interactions are allowed
PREDICTORS <- c("age")
PARENTS <- c("survived", "parch")
example4 <- function(degree, pred, parents, namesx)
{
if (degree > 1) {
predictor <- namesx[pred]
parents <- namesx[parents != 0]
if((any(predictor %in% PREDICTORS) && any(parents %in% PARENTS)) ||
(any(predictor %in% PARENTS) && any(parents %in% PREDICTORS))) {
return(FALSE)
}
}
TRUE
}
a4 <- earth(sex~., data=etitanic, degree=2, allowed=example4)
plotmo(a4)
#--- predictors in PREDICTORS are allowed to interact with predictors in PARENTS
#--- but no other interactions are allowed
PREDICTORS <- c("age")
PARENTS <- c("survived", "parch")
example5 <- function(degree, pred, parents, namesx)
{
if (degree <= 1)
return(TRUE)
predictor <- namesx[pred]
parents <- namesx[parents != 0]
if((any(predictor %in% PREDICTORS) && any(parents %in% PARENTS)) ||
(any(predictor %in% PARENTS) && any(parents %in% PREDICTORS))) {
return(TRUE)
}
FALSE
}
a5 <- earth(sex~., data=etitanic, degree=2, allowed=example5)
plotmo(a5)
7.3 허용 인수에 대한 자세한 사항(Further notes on the allowed argument)
기본 MARS 모델의 생성 전략은 allowed 함수가 있을 때에도 언제나 적용된다. 예를 들어, earth는 새로운 하나를 제외한 모든 펙터가 모델에 있는 경우에만 추가 조건을 고려한다. 이것은 allowed 함수가 억제한다는 의미이다, 말하자면, 모두 도수(degree) 2인 조건은 또한 효과적으로 더 높은 도수(degree) 역시 금지한다, 왜냐하면 earth가 도수(degree) 3으로 확장하기 위한 도수(degree) 2인 조건이 없을 것이다.
8 fda 와 mda 를 가지고 earth 사용
(Using earth with fda and mda)
Earth는 mda 패키지에 있는 fda 와 mda를 가지고 사용할 수 있다[13]. Earth는 이러한 함수로 호출될 때 다중 응답을 생성할 것이다. fda 호출에서 그들을 포함하여 earth에 degree=2 처럼 인수를 전달할 수 있다.
나중에 plotmo 호출을 원한다면 earth 인수 keepxy=TRUE를 사용해라. 나중에 plot.earth 호출을 원한다면 fda/mda 인수 keep.fitted=TRUE를 사용해라(실제로 큰 데이터셋을 위해서만 필요, fda 도움말 페이지에서 keep.fitted의 설명을 보라).
library(mda) (fda <- fda(Species~., data=iris, keep.fitted=TRUE, method=earth, keepxy=TRUE)) summary(fda$fit) # examine earth model embedded in fda model plot(fda) # right side of the figure
plotmo 사용으로 다음과 같이 우리는 fda의 예측자당 의존을 그릴 수 있다.
plotmo(fda, type="variates", nresponse=1, clip=F) # 1st disc var (Figure 5) plotmo(fda, type="variates", nresponse=2, clip=F) # 2nd disc var (not shown)
FDA모델에서 포함된 earth 모델을 볼 수 있다.
plotmo(fda$fit, nresponse=1, clip=F) # earth in FDA, 1st disc var (Figure 6) plotmo(fda$fit, nresponse=2, clip=F) # earth in FDA, 2nd disc var (not shown)
 |
| Figure 4: 선형의 하위모델(linear submodel)을 가지는 FDA의 plotmo 그래프(Figure 3의 왼쪽).
그래프는 첫번째 판별 변수에서 각 예측자의 기여도를 보여준다. 두번째 판별 변수는 여기에 보여주지 않는다. (그림을 생성하는 코드는 텍스트에 없다.) |
 |
| Figure 5: plotmo는 earth 하위모델을 가지는 FDA의 그래프이다(Figure 3의 오른쪽). 이 그래프는 첫번째 판별 변수에서 각 예측자의 기여도를 보여준다. |
 |
| Figure 6: FDA모델에서 포함된 earth 모델의 plotmo 그래프이다(점수화(scoring) 전의 첫번째 판별 변수). Earth는 Sepal.Width를 포함하지 않는다. |
8.1 유연한 판별 분석에 대한 간단한 소개
(A short introduction to Flexible Discriminant Analysis)
유연한 판별 분석(Flexible Discriminant Analysis: FDA)은 스테로이드에 선형 판별 분석(Linear Discriminant Analysis: LDA)이다. LDA는 분류를 나누기 위해 초평면을 사용한다. FDA는 분류를 더 잘 나누기 위해 곡선 또는 구부러진 표면을 가지고 이 초평면을 대체한다. 이것을 달성하기 위해 사용된 FDA 트릭은 분류 문제를 회귀 문제로 변경한다. 이것은 우리에서 판별 표면을 생성하기 위해 어떤 회귀 함수의 연결을 허용한다. 만약 선형 회귀 함수를 연결하면, FDA는 단지 LDA 같은 초평면을 생성할 것이다. earth에 연결하면, FDA는 MARS의 경첩(hinge) 함수로 정의된 표면을 생성할 것이다.
FDA는 분류 문제를 최적 점수(optimal scoring)를 통해서 회귀문제로 변환한다(Figure 7). 본질적으로, 이것은 본래의 응답에서 펙터 수준에 새로운 숫자를 할당하여 새로운 응답을 만든다. 그래서 예를 들면 setosa=1, versicolor=2, 그리고 virginica=3은 setosa=1.2, versicolor=-1.2, 그리고 virginica=0 이 될 것이다.
 |
| Figure 7: 왼쪽: 3개의 응답 범주를 가진 어떤 장난 데이터.
오른쪽: 재점수화(rescoring)는 각 범주에 새로운 숫자로 할당한다 그리서 데이터는 선형 분류의 더 좋은 형태가 된다. |
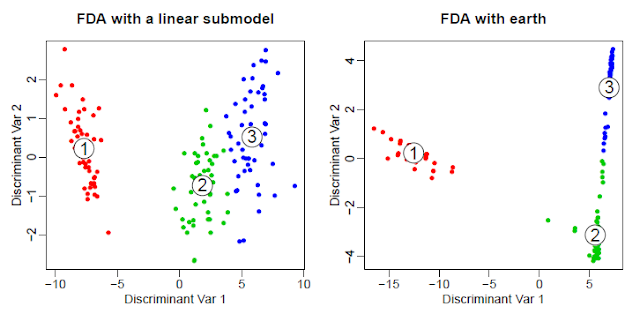
실제로, FDA는 각각 그 자신의 점수 집합을 가지고 몇개의 응답 변수를 만든다. 만약 K 개의 응답 분류가 있으면, FDA는 K- 1 개의 변수를 만든다. 그래서 붓꽃 데이터셋을 위해, 3개의 분류를 가짐(또는 R 용어에서 "수준(level)"), 우리는 3개의 판별 변수를 가진다(Figure 3). 이진 응답(binary response) FDA를 위해서는 하나의 판별 변수를 만든다, 그리고 판별공간은 하나의 차원이다. 판별 공간의 차원은 분류의 수에 의존한다는 것을 주의하라, 예측자의 수가 아님 - 차원 축소(dimensionality reduction)의 좋은 예. 때로는 독립적인 데이터에서 최적의 예측 결과는 만약 우리가 판별 변수의 단지 일부만 사용한다면 얻을 수 있다, 그리고 그러므로 차원의 더 많은 축소가 가능하다.
FDA 사용은 2개의 수준 보다 더 많이 가지고 있는 펙터의 응답을 위해 일반적으로 추천한다, 인자 행렬(indicator matrix)에서 직접 lm 또는 earth 같은 회귀 함수를 사용하는 것 보다. 이것은 "차단 문제(masking problem)"이기 때문이다((e.g. Hastie et al. [12] Section 4.2 "Linear Regression of an Indicator Matrix"). 실제로 최선의 충고는 이것을 시도하고 그리고 당신의 데이터에서 더 좋은 결과를 얻을 수 있는지 보라.
FDA의 2개의 이점은 (i) FDA는 LDA (또는 QDA) 보다 자주 더 잘 수행한다 왜냐하면 이것은 분류를 구분하기 위해 유연한 표면을 생성하기 때문이다, 그리고 (ii) 2 수준보다 더 많은 응답에서, FDA는 인자 행렬(indicator matrix)에서 회귀보다 종종 더 잘 수행할 것이다 왜냐하면 이것은 차단 문제(masking problem)를 격지 않는다.
우리는 "유연한 판별 분석(Flexible Discriminant Analysis)"의 약어 FDA 함수 데이터 분석(Functional Data Analysis)"와 같은 약어와 혼동하지 않을 것이다[23].
TODO 언제 FDA는 LDA와 정확하게 같게 되는가?
댓글 없음:
댓글 쓰기